练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若n≥6时，有(1-
    1
    n+3
    )    n    ＜
    1
    2
    ，则在m∈N*时，下列不等式成立的是（　　）
    A、(1-
    m
    n+3
    )    n    ≤(
    1
    2
    )    m
    B、(1-
    m
    n+3
    )    n    ≥(
    1
    2
    )    m
    C、(1-
    m
    n+3
    )    n    ＜(
    1
    2
    )    m
    D、(1-
    m
    n+3
    )    n    ＞(
    1
    2
    )    m
    分析：根据n≥6时，有(1-
    1
    n+3
    )    n    ＜
    1
    2
    ，结合选项，即可得出结论．
    解答：解：∵n≥6时，有(1-
    1
    n+3
    )    n    ＜
    1
    2
    ，
    ∴m=1时，(1-
    m
    n+3
    )n＜(
    1
    2
    )m    成立，
    故选C．
    点评：本题考查不等式的证明，考查学生分析解决问题的能力，属于基础题
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

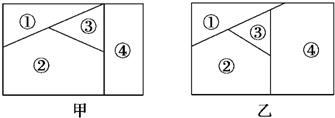    18、用n种不同颜色为下侧两块广告牌着色（如图甲、乙所示），要求在①、②、③、④四个区域中相邻（有公共边界）的区域不用同一种颜色．
    （1）若n=6，为甲着色时共有多少种不同方法？
    （2）若为乙着色时共有120种不同方法，求n．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

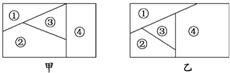    9、用n种不同的颜色为下列两块广告牌着色（如图甲、乙），要求在①②③④四个区域中相邻（有公共边界）的区域不用同一颜色．
    （1）若n=6，则为甲图着色的不同方法共有
    480
    种；
    （2）若为乙图着色时共有120种不同方法，则n=
    5
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

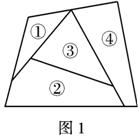
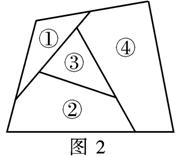
    有n种不同颜色为广告牌着色（如图），要求在①、②、③、④这4个区域中相邻(有公共边界)的区域不用同一种颜色.

           

    (1)当n=6时，为图1着色共有多少种不同的着色方法.

    (2)若为图2着色时共有120种不同的着色方法，求n.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某人骑自行车上班，第一条路线较短但拥挤，到达时间X(分钟)服从正态分布N(5,1);第二条路较长不拥挤，X服从N(6,0.16).有一天她出发时离点名时间还有7分钟，问他应选哪一条路线？若离点名时间还有6.5分钟，问他应选哪一条路线？

    查看答案和解析>>

    同步练习册答案