
直四棱柱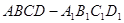 中,底面
中,底面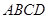 是等腰梯形,
是等腰梯形,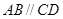 ,
,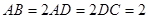 ,
, 为
为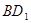 的中点,
的中点,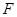 为
为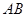 中点.
中点.
(1) 求证: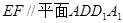 ;
;
(2) 若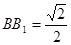 ,求
,求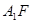 与平面
与平面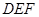 所成角的大小
所成角的大小
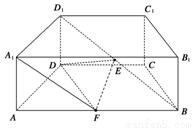
(1)证明:连结AD1,在△ABD1中
∵E是BD1的中点,F是BA中点,
∴EF//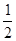 AD1
AD1
又EF⊄平面ADD1A1,AD1⊂平面ADD1A1
∴EF∥平面ADD1A1.
(2)解法1:延长D1A1至H,使A1H=D1A1,延长DA至G,使AG=DA,并连结HG和A1G,则A1G∥D1A∥EF
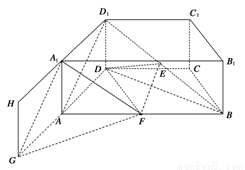
∴A1G∥平面DEF,
∴A1到平面DEF的距离等于G到平面DEF的距离,设为x
由题意可得,DF=BC=AD=1,连DB,在Rt△D1DB中,DE=D1B
又DB=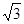 ,且DD1=
,且DD1=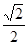 ,
,
∴DE=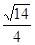 ,
,
又EF=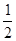 AD1=
AD1=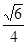 ,
,
在△DEF中,由余弦定理得:
cos∠EDF=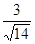
∴S△DEF=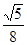 ,
,
又点E到平面DGF的距离d=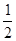 DD1=
DD1=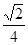
不难证明∠DFG是Rt△(∵FA=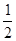 DG)
DG)
∴S△DFG=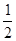 ×DF×FG=
×DF×FG=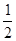 ×1×
×1×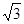
由VE-DGF=VG-DEF得,x·S△DEF=d·S△DFG,
∴即A1到平面DEF的距离为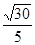 ,
,
设A1F与平面DEF成α角,则
sinα=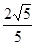 ,∴α=arcsin
,∴α=arcsin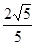 ,
,
即A1F与平面DEF所成角的大小为arcsin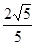 .
.
【解析】略


科目:高中数学 来源:名师指点学高中课程 数学 高二(下) 题型:013
以下各几何体中,是长方体的为
[ ]
查看答案和解析>>
科目:高中数学 来源:2010年甘肃省高二下学期期末考试数学卷 题型:选择题
下列几何体中,一定是长方体的是( )
A.直平行六面体 B.对角面为全等矩形的四棱柱
C.底面是矩形的直棱柱 D.侧面是矩形的四棱柱
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com