
【题目】甲、乙两所学校高三年级分别有1 200人,1 000人,为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况,采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩,并作出了频数分布统计表如下:
甲校:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 3 | 4 | 8 | 15 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 15 | x | 3 | 2 |
乙校:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 1 | 2 | 8 | 9 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 10 | 10 | y | 3 |
则x,y的值分别为( )
(A)、12,7 (B)、 10,7 (C)、 10,8 (D)、 11,9
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】关于函数![]() ,下列说法错误的是( )
,下列说法错误的是( )
A. ![]() 是
是![]() 的极小值点 B. 函数
的极小值点 B. 函数![]() 有且只有1个零点
有且只有1个零点
C. 存在正实数![]() ,使得
,使得![]() 恒成立 D. 对任意两个正实数
恒成立 D. 对任意两个正实数![]() ,且
,且![]() ,若
,若![]() ,则
,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值;
的距离的最大值;
(Ⅱ)若曲线![]() 上的所有点都在直线
上的所有点都在直线![]() 的下方,求实数
的下方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD和ADPQ均为正方形,他们所在的平面互相垂直,动点M在线段PQ上,E,F分别为AB,BC的中点,设异面直线EM与AF所成的角为θ,则cosθ的最大值为 . 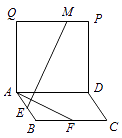
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a. 
(1)求a的值;
(2)求平面A1BC1与平面B1BC1所成的锐二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,实数
,实数![]() 为常数).
为常数).
(1)若![]() ,且函数
,且函数![]() 在
在![]() 上的最小值为0,求
上的最小值为0,求![]() 的值;
的值;
(2)若对于任意的实数![]() ,函数
,函数![]() 在区间
在区间![]() 上总是减函数,对每个给定的
上总是减函数,对每个给定的![]() ,求
,求![]() 的最大值
的最大值![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD是边长为1的菱形, ![]() 底面ABCD,SA=2,M为SA的中点.
底面ABCD,SA=2,M为SA的中点. 
(1)求异面直线AB与MD所成角的大小;
(2)求直线AS与平面SCD所成角的正弦值;
(3)求平面SAB与平面SCD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知动直线l过点 ![]() ,且与圆O:x2+y2=1交于A、B两点.
,且与圆O:x2+y2=1交于A、B两点. 
(1)若直线l的斜率为 ![]() ,求△OAB的面积;
,求△OAB的面积;
(2)若直线l的斜率为0,点C是圆O上任意一点,求CA2+CB2的取值范围;
(3)是否存在一个定点Q(不同于点P),对于任意不与y轴重合的直线l,都有PQ平分∠AQB,若存在,求出定点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com