
定义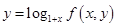 ,
, ,
,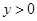 .
.
(1)比较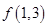 与
与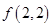 的大小;
的大小;
(2)若 ,证明:
,证明: ;
;
(3)设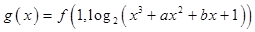 的图象为曲线
的图象为曲线 ,曲线
,曲线 在
在 处的切线斜率为
处的切线斜率为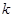 ,若
,若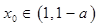 ,且存在实数
,且存在实数 ,使得
,使得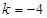 ,求实数
,求实数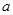 的取值范围.
的取值范围.
(1)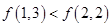 ;(2)详见解析;(3)实数
;(2)详见解析;(3)实数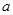 的取值范围为
的取值范围为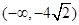 .
.
解析试题分析:(1)根据定义求出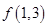 和
和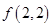 ,进而比较出
,进而比较出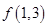 和
和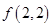 的大小;(2)先利用定义求出
的大小;(2)先利用定义求出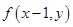 和
和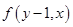 的表达式
的表达式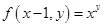 ,
,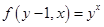 ,利用分析法将所要证明的不等式等价转化为
,利用分析法将所要证明的不等式等价转化为 ,构造新函数
,构造新函数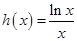 ,问题等价转化利用导数证明函数
,问题等价转化利用导数证明函数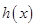 在区间
在区间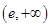 上单调递减;(3)先利用定义求出函数
上单调递减;(3)先利用定义求出函数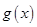 的解析式,并求出相应的导数,从而得到
的解析式,并求出相应的导数,从而得到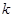 的表达式,结合对数运算将问题等价转化为不等式
的表达式,结合对数运算将问题等价转化为不等式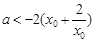 在
在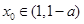 有解,结合导数对函数
有解,结合导数对函数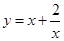 的极值点是否在区间
的极值点是否在区间 进行分类讨论,确定函数
进行分类讨论,确定函数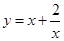 在区间
在区间 的最值,利用最值进行分析,从而求出参数
的最值,利用最值进行分析,从而求出参数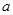 的取值范围.
的取值范围.
试题解析:(1)由定义知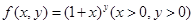
∴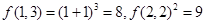 ,∴
,∴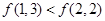 .
.
(2)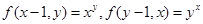
要证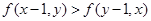 ,只要证
,只要证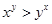
∵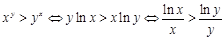
令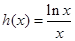 ,则
,则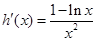 ,
,
当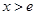 时,
时,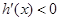 ,∴
,∴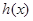 在
在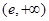 上单调递减.
上单调递减.
∵ ∴
∴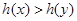 ,即
,即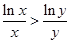
∴不等式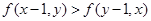 成立.
成立.
(3)由题意知: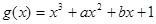 ,且
,且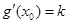
于是有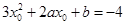 在
在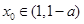 上有解.
上有解.
又由定义知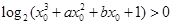 即
即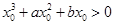
∵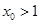 ∴
∴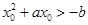 ,∴
,∴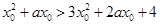 ,即
,即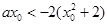
∴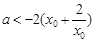 在
在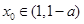 有解.
有解.
设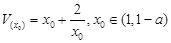
①当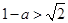 即
即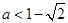 时,
时,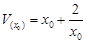 ≥
≥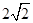 . 当且仅当
. 当且仅当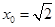 时,
时,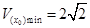
∴ 当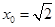 时,
时,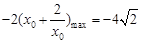 ∴
∴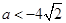
②当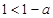 ≤
≤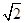 时,即
时,即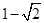 ≤
≤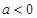 时,
时,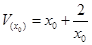 在
在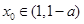 上递减,
上递减,
∴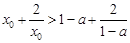 . ∴
. ∴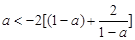
整理得: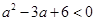 ,无解
,无解
综上所述,实数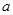 的取值范围为
的取值范围为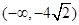 .
.
考点:1.新定义;2.利用分析法证明不等式;3.参数分离法;4.基本不等式


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:解答题
某商场经营一批进价是30元/件的商品,在市场试销中发现,此商品销售价 元与日销售量
元与日销售量 件之间有如下关系:
件之间有如下关系:
| x | 45 | 50 |
| y | 27 | 12 |
 与
与 的一个一次函数关系式
的一个一次函数关系式 ;
; 的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?
的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,h(x)=2alnx,
,h(x)=2alnx,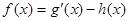 .
.
(1)当a∈R时,讨论函数 的单调性;
的单调性;
(2)是否存在实数a,对任意的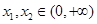 ,且
,且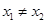 ,都有
,都有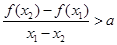
恒成立,若存在,求出a的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一条笔直的工艺流水线上有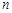 个工作台,将工艺流水线用如图
个工作台,将工艺流水线用如图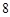 所示的数轴表示,各工作台的坐标分别为
所示的数轴表示,各工作台的坐标分别为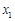 ,
,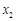 ,
,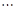 ,
,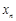 ,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.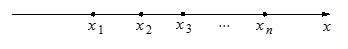
(Ⅰ)若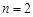 ,每个工作台上只有一名工人,试确定供应站的位置;
,每个工作台上只有一名工人,试确定供应站的位置;
(Ⅱ)若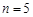 ,工作台从左到右的人数依次为
,工作台从左到右的人数依次为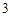 ,
,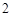 ,
,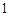 ,
,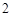 ,
,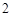 ,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了降低能源损耗,某体育馆的外墙需要建造隔热层.体育馆要建造可使用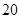 年的隔热层,每厘米厚的隔热层建造成本为
年的隔热层,每厘米厚的隔热层建造成本为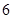 万元.该建筑物每年的能源消耗费用
万元.该建筑物每年的能源消耗费用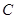 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度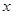 (单位:
(单位: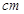 )满足关系:
)满足关系: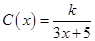 (
(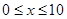 ,
, 为常数),若不建隔热层,每年能源消耗费用为
为常数),若不建隔热层,每年能源消耗费用为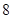 万元.设
万元.设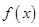 为隔热层建造费用与
为隔热层建造费用与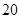 年的能源消耗费用之和.
年的能源消耗费用之和.
(1)求 的值及
的值及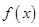 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用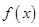 达到最小,并求最小值.
达到最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一种放射性元素,最初的质量为 ,按每年
,按每年 衰减.
衰减.
(1)求 年后,这种放射性元素的质量
年后,这种放射性元素的质量 与
与 的函数关系式;
的函数关系式;
(2)求这种放射性元素的半衰期(质量变为原来的 时所经历的时间).(
时所经历的时间).( )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示, 是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛
是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛 扩建成一个更大的矩形花园
扩建成一个更大的矩形花园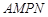 ,要求:B在
,要求:B在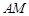 上,D在
上,D在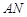 上,对角线
上,对角线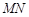 过C点,且矩形
过C点,且矩形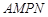 的面积小于64平方米.
的面积小于64平方米.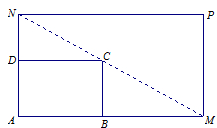
(Ⅰ)设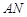 长为
长为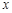 米,矩形
米,矩形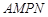 的面积为
的面积为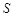 平方米,试用解析式将
平方米,试用解析式将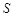 表示成
表示成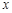 的函数,并写出该函数的定义域;
的函数,并写出该函数的定义域;
(Ⅱ)当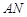 的长度是多少时,矩形
的长度是多少时,矩形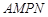 的面积最小?并求最小面积.
的面积最小?并求最小面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com