
ЁОЬтФПЁПТжДЌ![]() ДгФГИлПкНЋвЛаЉЮяЦЗЫЭЕНе§КНааЕФТжДЌ
ДгФГИлПкНЋвЛаЉЮяЦЗЫЭЕНе§КНааЕФТжДЌ![]() ЩЯЃЌдкТжДЌ
ЩЯЃЌдкТжДЌ![]() ГіЗЂЪБЃЌТжДЌ
ГіЗЂЪБЃЌТжДЌ![]() ЮЛгкИлПк
ЮЛгкИлПк![]() ББЦЋЮї
ББЦЋЮї![]() Чвгы
Чвгы![]() ЯрОр20КЃРяЕФ
ЯрОр20КЃРяЕФ![]() ДІЃЌВЂе§вд30КЃРяЕФКНЫйбие§ЖЋЗНЯђдШЫйааЪЛЃЌМйЩшТжДЌ
ДІЃЌВЂе§вд30КЃРяЕФКНЫйбие§ЖЋЗНЯђдШЫйааЪЛЃЌМйЩшТжДЌ![]() бижБЯпЗНЯђвд
бижБЯпЗНЯђвд![]() КЃРя/аЁЪБЕФКНЫйдШЫйааЪЛЃЌОЙ§
КЃРя/аЁЪБЕФКНЫйдШЫйааЪЛЃЌОЙ§![]() аЁЪБгыТжДЌ
аЁЪБгыТжДЌ![]() Яргі.
Яргі.
ЃЈ1ЃЉШєЪЙЯргіЪБТжДЌ![]() КНОрзюЖЬЃЌдђТжДЌ
КНОрзюЖЬЃЌдђТжДЌ![]() ЕФКНааЫйЖШДѓаЁгІЮЊЖрЩйЃП
ЕФКНааЫйЖШДѓаЁгІЮЊЖрЩйЃП
ЃЈ2ЃЉМйЩшТжДЌ![]() ЕФзюИпКНЫйжЛФмДяЕН30КЃРя/аЁЪБЃЌдђТжДЌ
ЕФзюИпКНЫйжЛФмДяЕН30КЃРя/аЁЪБЃЌдђТжДЌ![]() вдЖрДѓЫйЖШМАЪВУДКНааЗНЯђВХФмдкзюЖЬЪБМфгыТжДЌ
вдЖрДѓЫйЖШМАЪВУДКНааЗНЯђВХФмдкзюЖЬЪБМфгыТжДЌ![]() ЯргіЃЌВЂЫЕУїРэгЩ.
ЯргіЃЌВЂЫЕУїРэгЩ.
ЁОД№АИЁПЃЈ1ЃЉТжДЌ![]() вд
вд![]() КЃРя/аЁЪБЕФЫйЖШКНааЃЌЯргіЪБТжДЌ
КЃРя/аЁЪБЕФЫйЖШКНааЃЌЯргіЪБТжДЌ![]() КНОрзюЖЬЃЛЃЈ2ЃЉКНЯђЮЊББЦЋЖЋ
КНОрзюЖЬЃЛЃЈ2ЃЉКНЯђЮЊББЦЋЖЋ![]() ЃЌКНЫйЮЊ30КЃРя/аЁЪБЃЌТжДЌ
ЃЌКНЫйЮЊ30КЃРя/аЁЪБЃЌТжДЌ![]() ФмдкзюЖЬЪБМфгыТжДЌ
ФмдкзюЖЬЪБМфгыТжДЌ![]() Яргі.
Яргі.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЩшСНТжДЌдк![]() ДІЯргіЃЌдк
ДІЯргіЃЌдк![]() жаЃЌРћгУгрЯвЖЈРэЕУГі
жаЃЌРћгУгрЯвЖЈРэЕУГі![]() ЙигкtЕФКЏЪ§ЃЌДгЖјЕУГі
ЙигкtЕФКЏЪ§ЃЌДгЖјЕУГі![]() ЕФзюаЁжЕМАЦфЖдгІЕФ
ЕФзюаЁжЕМАЦфЖдгІЕФ![]() ЃЌЕУГіЫйЖШЃЛ
ЃЌЕУГіЫйЖШЃЛ
ЃЈ2ЃЉРћгУгрЯвЖЈРэМЦЫуКНааЪБМф![]() ЃЌЕУГі
ЃЌЕУГі![]() ОрРыЃЌДгЖјЕУГі
ОрРыЃЌДгЖјЕУГі![]() ЕФЖШЪ§ЃЌЕУГіКНааЗНАИЃЎ
ЕФЖШЪ§ЃЌЕУГіКНааЗНАИЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЩшЯргіЪБТжДЌ![]() КНааЕФОрРыЮЊ
КНааЕФОрРыЮЊ![]() КЃРяЃЌдђ
КЃРяЃЌдђ
![]()
![]()
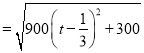 .
.
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЃЌ
ЃЌ 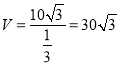 ЃЌ
ЃЌ
МДТжДЌ![]() вд
вд![]() КЃРя/аЁЪБЕФЫйЖШКНааЃЌЯргіЪБТжДЌ
КЃРя/аЁЪБЕФЫйЖШКНааЃЌЯргіЪБТжДЌ![]() КНОрзюЖЬ.
КНОрзюЖЬ.
ЃЈ2ЃЉЩшТжДЌ![]() гыТжДЌ
гыТжДЌ![]() дк
дк![]() ДІЯргіЃЌдђ
ДІЯргіЃЌдђ![]()
![]() ЃЌ
ЃЌ
МД![]() .
.
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌгж
ЃЌгж![]() ЪБ
ЪБ![]() ЃЌ
ЃЌ
Ёр![]() ЪБЃЌ
ЪБЃЌ ![]() зюаЁЧвЮЊ
зюаЁЧвЮЊ![]() ЃЌДЫЪБ
ЃЌДЫЪБ![]() жа
жа![]() ЃЌ
ЃЌ
ЁрКНЯђЮЊББЦЋЖЋ![]() ЃЌКНЫйЮЊ30КЃРя/аЁЪБЃЌ
ЃЌКНЫйЮЊ30КЃРя/аЁЪБЃЌ
ТжДЌ![]() ФмдкзюЖЬЪБМфгыТжДЌ
ФмдкзюЖЬЪБМфгыТжДЌ![]() Яргі.
Яргі.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈЂёЃЉЕБ![]() ЪБЃЌЧѓЧњЯп
ЪБЃЌЧѓЧњЯп![]() дкЕу
дкЕу![]() ДІЕФЧаЯпЗНГЬЃЛ
ДІЕФЧаЯпЗНГЬЃЛ
ЃЈЂђЃЉШє![]() КуГЩСЂЃЌЧѓ
КуГЩСЂЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈЂѓЃЉжЄУїЃКзмДцдк![]() ЃЌЪЙЕУЕБ
ЃЌЪЙЕУЕБ![]() ЃЌКуга
ЃЌКуга![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЙњМвЁАДѓжкДДвЕЃЌЭђжкДДаТЁБеНТдЯТЃЌФГЦѓвЕОіЖЈМгДѓЖдФГжжВњЦЗЕФбаЗЂЭЖШыЃЌвбжЊбаЗЂЭЖШы![]() (ЪЎЭђдЊ)гыРћШѓ
(ЪЎЭђдЊ)гыРћШѓ![]() (АйЭђдЊ)жЎМфгаШчЯТЖдгІЪ§ОнЃК
(АйЭђдЊ)жЎМфгаШчЯТЖдгІЪ§ОнЃК
| 2 | 3 | 4 | 5 | 6 |
| 2 | 4 | 5 | 6 | 7 |
ШєгЩзЪСЯжЊ![]() Жд
Жд![]() ГЪЯпадЯрЙиЙиЯЕЁЃЪдЧѓЃК
ГЪЯпадЯрЙиЙиЯЕЁЃЪдЧѓЃК
ЃЈ1ЃЉЯпадЛиЙщЗНГЬ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЙРМЦ![]() ЪБЃЌРћШѓЪЧЖрЩйЃП
ЪБЃЌРћШѓЪЧЖрЩйЃП
ИНЃКРћгУЁАзюаЁЖўГЫЗЈЁБМЦЫуa,bЕФжЕЪБ,ПЩИљОнвдЯТЙЋЪНЃК
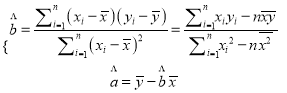
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛЦћГЕГЇЩњВњAЃЌBЃЌCШ§РрНЮГЕЃЌУПРрНЮГЕОљгаЪцЪЪаЭКЭБъзМаЭСНжжаЭКХЃЌФГдТВњСПШчБэЃЈЕЅЮЛЃКСОЃЉЃК
НЮГЕA | НЮГЕB | НЮГЕC | |
ЪцЪЪаЭ | 100 | 150 | z |
БъзМаЭ | 300 | 450 | 600 |
АДРраЭЗжВуГщбљЕФЗНЗЈдкетИідТЩњВњЕФНЮГЕжаГщШЁ50СОЃЌЦфжагаAРрНЮГЕ10СОЁЃ
ЃЈ1ЃЉЧѓzЕФжЕЃЛ
ЃЈ2ЃЉгУЗжВуГщбљЕФЗНЗЈдкCРрНЮГЕжаГщШЁвЛИіШнСПЮЊ5ЕФбљБОЁЃНЋИУбљБОПДГЩвЛИізмЬхЃЌДгжаШЮШЁ2СОЃЌЧѓжСЩйга1СОЪцЪЪаЭНЮГЕЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
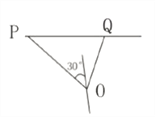
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯп![]() ЕФНЙЕуЮЊ
ЕФНЙЕуЮЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() Й§
Й§![]() ЧввРДЮНЛХзЮяЯпМАдВ
ЧввРДЮНЛХзЮяЯпМАдВ![]() гкЕу
гкЕу![]() ЫФЕуЃЌдђ
ЫФЕуЃЌдђ![]() ЕФзюаЁжЕЮЊЃЈ ЃЉ
ЕФзюаЁжЕЮЊЃЈ ЃЉ

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаИїзщКЏЪ§жаЃЌБэЪОЭЌвЛКЏЪ§ЕФЪЧЃЈ ЃЉ
A.fЃЈxЃЉ=xЉ1ЃЌgЃЈxЃЉ= ![]() Љ1
Љ1
B.fЃЈxЃЉ=|x|ЃЌgЃЈxЃЉ=ЃЈ ![]() ЃЉ2
ЃЉ2
C.fЃЈxЃЉ=xЃЌgЃЈxЃЉ= ![]()
D.fЃЈxЃЉ=2xЃЌgЃЈxЃЉ= ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшХМКЏЪ§fЃЈxЃЉТњзуfЃЈxЃЉ=x3Љ8ЃЈxЁн0ЃЉЃЌдђ{x|fЃЈxЉ2ЃЉЃО0}=ЃЈ ЃЉ
A.{x|xЃМЉ2ЛђxЃО4}
B.{x|xЃМ0ЛђxЃО4}
C.{x|xЃМ0ЛђxЃО6}
D.{x|xЃМЉ2ЛђxЃО2}
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌаБШ§Ртжљ![]() жаЃЌВрУц
жаЃЌВрУц![]() ЮЊСтаЮЃЌЕзУц
ЮЊСтаЮЃЌЕзУц![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЪЧЕШбќжБНЧШ§НЧаЮЃЌ ![]() .
.

ЃЈ1ЃЉЧѓжЄЃКжБЯп![]() жБЯп
жБЯп![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєжБЯп![]() гыЕзУц
гыЕзУц![]() ГЩЕФНЧЮЊ60ЁуЃЌЧѓЖўУцНЧ
ГЩЕФНЧЮЊ60ЁуЃЌЧѓЖўУцНЧ![]() ЕФгрЯвжЕЃЎ
ЕФгрЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=ax2Љx+2aЉ1ЃЈaЃО0ЃЉЃЎ
ЃЈ1ЃЉШєfЃЈxЃЉдкЧјМф[1ЃЌ2]ЮЊЕЅЕїдіКЏЪ§ЃЌЧѓaЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЩшКЏЪ§fЃЈxЃЉдкЧјМф[1ЃЌ2]ЩЯЕФзюаЁжЕЮЊgЃЈaЃЉЃЌЧѓgЃЈaЃЉЕФБэДяЪНЃЛ
ЃЈ3ЃЉЩшКЏЪ§ ![]() ЃЌШєЖдШЮвтx1 ЃЌ x2ЁЪ[1ЃЌ2]ЃЌВЛЕШЪНfЃЈx1ЃЉЁнhЃЈx2ЃЉКуГЩСЂЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЎ
ЃЌШєЖдШЮвтx1 ЃЌ x2ЁЪ[1ЃЌ2]ЃЌВЛЕШЪНfЃЈx1ЃЉЁнhЃЈx2ЃЉКуГЩСЂЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com