
已知 的边
的边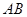 所在直线的方程为
所在直线的方程为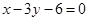 ,
,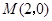 满足
满足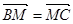 , 点
, 点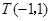 在
在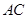 所在直线上且
所在直线上且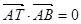 .
.
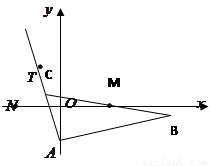
(Ⅰ)求 外接圆的方程;
外接圆的方程;
(Ⅱ)一动圆过点 ,且与
,且与 的
的
外接圆外切,求此动圆圆心的轨迹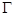 的方程;
的方程;
(Ⅲ)过点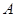 斜率为
斜率为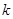 的直线与曲线
的直线与曲线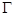 交于相异的
交于相异的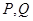 两点,满足
两点,满足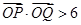 ,求
,求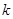 的取值范围.
的取值范围.
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com