
【题目】己知函数![]() ,
, ![]() .
.
(I)求函数![]() 的单调区间;
的单调区间;
(II)设![]() ,已知函数
,已知函数![]() 在
在![]() 上是增函数.
上是增函数.
(1)研究函数![]() 上零点的个数;
上零点的个数;
(ii)求实数c的取值范围.
【答案】(Ⅰ)详见解析; (Ⅱ)(1)1个;(2) ![]() .
.
【解析】试题分析(1) 对函数求导,①当![]() 时,
时, ![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数;②当
上是增函数;②当![]() 时,
时, ![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数;(2) (1)当
上是减函数;(2) (1)当![]() 时,函数
时,函数![]()
![]() ,
, ![]() ,
, ![]() 在
在![]() 上单调递减.又
上单调递减.又![]() ,
, ![]() ,由函数的零点存在性定理及其单调性知,
,由函数的零点存在性定理及其单调性知, ![]() 在
在![]() 上零点的个数为1.(2)由(1)知,当
上零点的个数为1.(2)由(1)知,当![]() 时,
时, ![]() >0,当
>0,当![]() 时,
时, ![]() <0.∴当
<0.∴当![]() 时,
时, ![]() =
=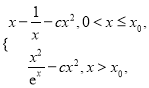 求导,得
求导,得![]() 在
在![]() ,
, ![]() 上恒成立. ①当
上恒成立. ①当![]() 时,
时, ![]() min=
min= ![]() 极小值=
极小值= ![]()
![]() ,故“
,故“![]() 在
在![]() 上恒成立”,只需
上恒成立”,只需![]()
![]() .②当
.②当![]() 时,当
时,当![]() 时,
时, ![]() 在
在![]() 上恒成立,综合①②知,
上恒成立,综合①②知, ![]() 的取值范围是
的取值范围是![]() .
.
试题解析:(Ⅰ)∵![]() ,
,
∴![]() ,
,
①当![]() 时,
时,
在![]() 时,
时, ![]() ,
,
在![]() 时,
时, ![]() ,
,
故![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数;
上是增函数;
②当![]() 时,
时,
在![]() 时,
时, ![]() ,
,
在![]() 时,
时, ![]() ,
,
故![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数;
上是减函数;
(Ⅱ)(1)当![]() 时,函数
时,函数![]()
![]() ,
,
求导,得![]() ,
,
当![]() 时,
时, ![]() 恒成立,
恒成立,
当![]() 时,
时, 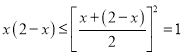 ,
,
∴![]()
![]() ,
,
∴![]() 在
在![]() 上恒成立,故
上恒成立,故![]() 在
在![]() 上单调递减.
上单调递减.
又![]() ,
, ![]() ,
,
曲线![]() 在[1,2]上连续不间断,
在[1,2]上连续不间断,
∴由函数的零点存在性定理及其单调性知,唯一的![]() ∈(1,2),使
∈(1,2),使![]() ,
,
所以,函数![]() 在
在![]() 上零点的个数为1.
上零点的个数为1.
(2)由(1)知,当![]() 时,
时, ![]() >0,当
>0,当![]() 时,
时, ![]() <0.
<0.
∴当![]() 时,
时, ![]() =
=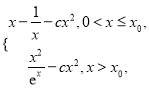
求导,得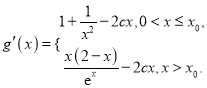
由函数![]() 在
在![]() 上是增函数,且曲线
上是增函数,且曲线![]() 在
在![]() 上连续不断知:
上连续不断知:
![]() 在
在![]() ,
, ![]() 上恒成立.
上恒成立.
①当![]() 时,
时, ![]()
![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,
上恒成立,
记![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
,
当 ![]() 变化时,
变化时, ![]() ,
, ![]() 变化情况列表如下:
变化情况列表如下:
| 3 |
| |
|
| 0 |
|
|
| 极小值 |
|
∴![]() min=
min= ![]() 极小值=
极小值= ![]()
![]() ,
,
故“![]() 在
在![]() 上恒成立”,只需
上恒成立”,只需![]()
![]() ,即
,即![]() .
.
②当![]() 时,
时, ![]()
![]() ,
,
当![]() 时,
时, ![]() 在
在![]() 上恒成立,
上恒成立,
综合①②知,当![]() 时,函数
时,函数![]() 在
在![]() 上是增函数.
上是增函数.
故实数![]() 的取值范围是
的取值范围是![]() .
.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:
【题目】我国科研人员屠呦呦法相从青篙中提取物青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间r(小时)之间近似满足如图所示的曲线 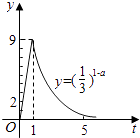
(1)写出第一服药后y与t之间的函数关系式y=f(x);
(2)据进一步测定:每毫升血液中含药量不少于 ![]() 微克时,治疗有效,求服药一次后治疗有效的时间是多长?
微克时,治疗有效,求服药一次后治疗有效的时间是多长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈[1,2],x2≥a;命题q:x∈R,x2+2ax+2﹣a=0,若命题p∧q是真命题,则实数a的取值范围是( )
A.a≤﹣2或a=1
B.a≤﹣2或1≤a≤2
C.a≥1
D.﹣2≤a≤1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位学生参加数学竞赛培训,他们在培训期间8次模拟考试的成绩如下: 甲:82 81 79 78 95 88 93 84
乙:92 95 80 75 83 80 90 85
(1)画出甲、乙两位学生成绩的茎叶图,并求学生乙成绩的平均数和方差;
(2)从甲同学超过80分的6个成绩中任取两个,求这两个成绩中至少有一个超过90分的概率.
(3)甲同学超过80(分)的成绩有82 81 95 88 93 84,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知中心在原点,焦点在![]() 轴上的椭圆的一个焦点为
轴上的椭圆的一个焦点为![]() ,
, 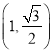 是椭圆上的一个点.
是椭圆上的一个点.
(1)求椭圆的标准方程;
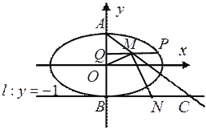
(2)设椭圆的上、下顶点分别为![]() ,
, ![]() (
(![]() )是椭圆上异于
)是椭圆上异于![]() 的任意一点,
的任意一点, ![]() 轴,
轴, ![]() 为垂足,
为垂足, ![]() 为线段
为线段![]() 中点,直线
中点,直线![]() 交直线
交直线![]() 于点
于点![]() ,
, ![]() 为线段
为线段![]() 的中点,如果
的中点,如果![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列{an}中,a1=3,其前n项和为Sn , 等比数列{bn}的各项均为正数,b1=1,公比为q(q≠0),且b2+S2=12, ![]() .
.
(1)求{an}与{bn}的通项公式;
(2)证明: ![]()
![]() +
+ ![]() +…+
+…+ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
空气质量指数 |
|
|
|
|
|
|
空气质量等级 |
|
|
污染 |
污染 |
污染 |
|
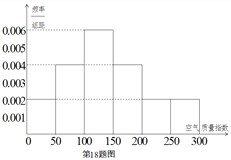
该社团将该校区在2016年100天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
(Ⅰ)请估算2017年(以365天计算)全年空气质量优良的天数(未满一天按一天计算);
(Ⅱ)用分层抽样的方法共抽取10天,则空气质量指数在(0,50],(50,100],(100,150]的天数中各应抽取几天?
(Ⅲ)已知空气质量等级为1级时不需要净化空气,空气质量等级为2级时每天需净化空气的费用为2000元,空气质量等级为3级时每天需净化空气的费用为4000元.若在(Ⅱ)的条件下,从空气质量指数在![]() 的天数中任意抽取两天,求这两天的净化空气总费用为4000元的概率.
的天数中任意抽取两天,求这两天的净化空气总费用为4000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M,N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S﹣ABCD的体积为V(x),则函数V(x)的图象是( ) 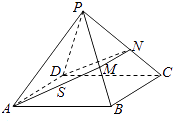
A.
B.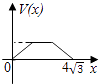
C.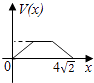
D.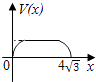
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com