�⣺��1��������ɵã���n��2ʱ����

��
��ʽ������� a
n+1 -a
n =2a
n����a
n+1=3a
n ��n��2��
���ԣ���n��2ʱ��{a
n}�ǵȱ����У�Ҫʹn��1ʱ{a
n}�ǵȱ����У�
��ֻ��
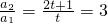
���Ӷ��ó�t=1��
��2���ɣ�1���ã��ȱ�����{a
n}������Ϊa
1=1������q=3����
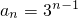
��
��
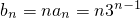
��
��
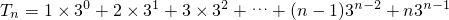
���٣�7�֣�
��ʽ���߳���3��

�ڣ�
��-�ڵ�

��
��
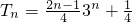
��
��3���ɣ�2��֪
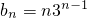
����

��
��

��
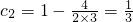
����c
1c
2=-1��0��
��
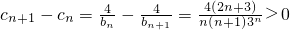
��������{c
n}������
��
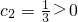
���õ�n��2ʱ��c
n��0��
������{c
n}�ġ����������Ϊ1��
��������1���������еĵ�n����ǰn��͵Ĺ�ϵ�ɵ�n��2ʱ����

�������a
n+1=3a
n ��n��2����Ҫʹn��1ʱ{a
n}�ǵȱ����У�ֻ��
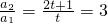
���Ӷ��ó�t��ֵ��
��2���ɣ�1���ã��ȱ�����{a
n}������Ϊa
1=1������q=3������
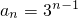
���Ӷ��õ�
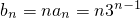
���ô�λ������������{b
n}��ǰn���T
n ��
��3�����������

������ɵ�c
1c
2=-1��0������c
n+1-c
n��0�ɵã�����{c
n}��������
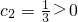
���õ�n��2ʱ��c
n��0���ɴ��������{c
n}�ġ����������Ϊ1��
������������Ҫ����ȱȹ�ϵ��ȷ�����ô�λ����������н�����ͣ����еĵ�n����ǰn��͵Ĺ�ϵ�������뺯�����ۺϣ��������⣮

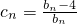 ��n��N*�����ڣ�2���������£�������{cn}�ġ������������
��n��N*�����ڣ�2���������£�������{cn}�ġ������������ ��
��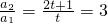 ���Ӷ��ó�t=1��
���Ӷ��ó�t=1��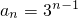 ��
��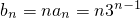 ��
��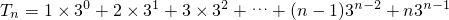 ���٣�7�֣�
���٣�7�֣� �ڣ�
�ڣ� ��
��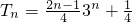 ��
��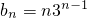 ����
���� ��
�� ��
��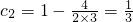 ����c1c2=-1��0��
����c1c2=-1��0��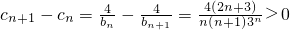 ��������{cn}������
��������{cn}������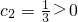 ���õ�n��2ʱ��cn��0��
���õ�n��2ʱ��cn��0�� �������an+1=3an ��n��2����Ҫʹn��1ʱ{an}�ǵȱ����У�ֻ��
�������an+1=3an ��n��2����Ҫʹn��1ʱ{an}�ǵȱ����У�ֻ��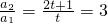 ���Ӷ��ó�t��ֵ��
���Ӷ��ó�t��ֵ��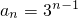 ���Ӷ��õ�
���Ӷ��õ�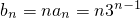 ���ô�λ������������{bn}��ǰn���Tn ��
���ô�λ������������{bn}��ǰn���Tn �� ������ɵ�c1c2=-1��0������cn+1-cn��0�ɵã�����{cn}��������
������ɵ�c1c2=-1��0������cn+1-cn��0�ɵã�����{cn}��������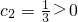 ���õ�n��2ʱ��cn��0���ɴ��������{cn}�ġ����������Ϊ1��
���õ�n��2ʱ��cn��0���ɴ��������{cn}�ġ����������Ϊ1��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�