
已知函数 ,设
,设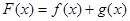
(Ⅰ)求函数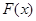 的单调区间
的单调区间
(Ⅱ)若以函数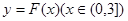 图象上任意一点
图象上任意一点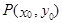 为切点的切线的斜率
为切点的切线的斜率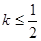 恒成立,求实数
恒成立,求实数 的最小值
的最小值
(Ⅲ)是否存在实数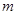 ,使得函数
,使得函数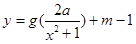 的图象与函数
的图象与函数 的图象恰有四个不同交点?若存在,求出实数
的图象恰有四个不同交点?若存在,求出实数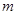 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
(Ⅰ) 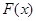 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为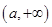 ;(Ⅱ)实数
;(Ⅱ)实数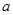 的最小值
的最小值 ;(Ⅲ)当
;(Ⅲ)当 时,
时,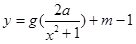 的图像与
的图像与 的图像恰有四个不同交点.
的图像恰有四个不同交点.
【解析】
试题分析:(I)求函数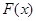 的单调区间,首先求出
的单调区间,首先求出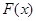 的解析式,得
的解析式,得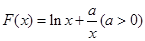 ,求函数
,求函数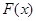 的单调区间,可用定义,也可用导数法,由于本题含有对数函数,可通过求导来求,对
的单调区间,可用定义,也可用导数法,由于本题含有对数函数,可通过求导来求,对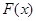 求导得
求导得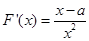 ,分别求出
,分别求出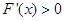 与
与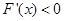 的范围,从而求出
的范围,从而求出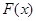 的单调区间;(II)若以函数
的单调区间;(II)若以函数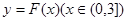 图象上任意一点
图象上任意一点 为切点的切线的斜率
为切点的切线的斜率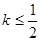 恒成立,求实数
恒成立,求实数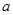 的最小值,可利用导数的几何意义表示出切线的斜率
的最小值,可利用导数的几何意义表示出切线的斜率 ,根据
,根据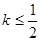 恒成立,将
恒成立,将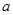 分离出来得
分离出来得 ,即
,即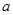 大于等于
大于等于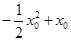 的最大值即可,这样求出
的最大值即可,这样求出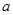 的范围,从而得到
的范围,从而得到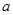 的最小值;(III)函数
的最小值;(III)函数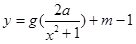 的图象与
的图象与 的图象有四个不同的交点,即方程
的图象有四个不同的交点,即方程 有四个不同的根,分离出
有四个不同的根,分离出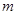 后,转化成新函数的极大值和极小值问题,利用图像即可求出实数
后,转化成新函数的极大值和极小值问题,利用图像即可求出实数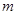 的取值范围.
的取值范围.
试题解析:(Ⅰ)F(x)=f(x)+g(x)=lnx+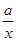 (x>0),
(x>0),
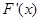 =
=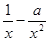 =
=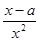
∵a>0,由FF'(x)>0Þx∈(a,+∞),∴F(x)在(a,+∞)上是增函数.
由FF'(x)<0Þx∈(0,a),∴F(x)在(0,a)上是减函数.
∴F(x)的单调递减区间为(0,a),单调递增区间为(a,+∞).
(Ⅱ)由FF'(x)=
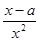 (0<x≤3)得
(0<x≤3)得
k= FF'(x0)= 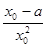 ≤
≤ (0<x0≤3)恒成立Ûa≥-
(0<x0≤3)恒成立Ûa≥- x02+x0恒成立.
x02+x0恒成立.
∵当x0=1时,- x02+x0取得最大值
x02+x0取得最大值
∴a≥ ,a的最小值为
,a的最小值为 .
.
(Ⅲ)若y=g(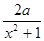 )+m-1=
)+m-1= x2+m-
x2+m- 的图像与y=f(1+x2)=ln(x2+1)的图像恰有四个不同交点,即
的图像与y=f(1+x2)=ln(x2+1)的图像恰有四个不同交点,即 x2+m-
x2+m- =ln(x2+1)有四个不同的根,亦即m=ln(x2+1)-
=ln(x2+1)有四个不同的根,亦即m=ln(x2+1)- x2+
x2+ 有四个不同的根.令
有四个不同的根.令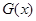 = ln(x2+1)-
= ln(x2+1)- x2+
x2+ .
.
则GF'(x)= -x=
-x=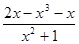 =
=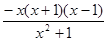
当x变化时GF'(x)、G(x)的变化情况如下表:
|
|
(-¥,-1) |
(-1,0) |
(0,1) |
(1,+¥) |
|
GF'(x)的符号 |
+ |
- |
+ |
- |
|
G(x)的单调性 |
↗ |
↘ |
↗ |
↘ |
由上表知:G(x)极小值=G(0)= ,
G(x)极大值=G(-1)=G(1)=ln2>0
,
G(x)极大值=G(-1)=G(1)=ln2>0
画出草图和验证G(2)=G(-2)=ln5-2+ <
< 可知,当m∈(
可知,当m∈( ,ln2)时,y=G(x)与y=m恰有四个不同交点.
,ln2)时,y=G(x)与y=m恰有四个不同交点.
∴当m∈( ,ln2)时,y=g(
,ln2)时,y=g(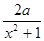 )+m-1=
)+m-1= x2+m-
x2+m- 的图像与y=f(1+x2)=ln(x2+1)的图像恰有四个不同交点.
的图像与y=f(1+x2)=ln(x2+1)的图像恰有四个不同交点.
考点:利用导数研究曲线上某点切线方程;利用导数研究函数的单调性;利用导数求闭区间上函数的最值.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源:2012-2013学年辽宁省五校协作体高三第二次模拟考试理科数学试卷(解析版) 题型:解答题
已知函数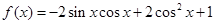
(1)设方程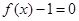 在(0,
在(0,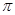 )内有两个零点
)内有两个零点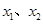 ,求
,求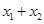 的值;
的值;
(2)若把函数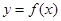 的图像向左移动
的图像向左移动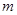
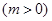 个单位,再向下平移2个单位,使所得函数的图象关于
个单位,再向下平移2个单位,使所得函数的图象关于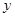 轴对称,求
轴对称,求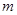 的最小值。
的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com