Question

求证：对于大于1的任意自然数n，都有．

Answer 1

【答案】分析：直接利用数学归纳法的证明步骤，验证n=2时不等式成立，然后假设n=k时不等式成立，证明n=k+1时不等式也成立即可．
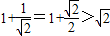
解答：证明：（1）当n=2时，左边=显然成立．（2分）
（2）假设n=k（k≥2且K∈N时，成立 （4分）
则当n=k+1时，． （5分）
又因为，
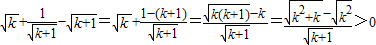
所以，即，
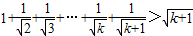
当n=k+1时，不等式也成立．（11分）
由（1）（2）可知对于大于1的任意自然数n，都有．     （12分）
点评：本题考查数学归纳法证明不等式的证明步骤，注意n=k+1时必须用上假设，考查逻辑推理能力．
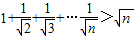