
【题目】已知点![]() ,
,![]() (其中
(其中![]() )是曲线
)是曲线![]() 上的两点,
上的两点,![]() ,
,![]() 两点在
两点在![]() 轴上的射影分别为点
轴上的射影分别为点![]() ,
,![]() 且
且![]() .
.
(1)当点![]() 的坐标为
的坐标为![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)记![]() 的面积为
的面积为![]() ,梯形
,梯形![]() 的面积为
的面积为![]() ,求
,求![]() 的范围.
的范围.
科目:高中数学 来源: 题型:
【题目】学校组织高考组考工作,为了搞好接待组委会招募了![]() 名男志愿者和
名男志愿者和![]() 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有![]() 人和
人和![]() 人喜爱运动,其余不喜爱.
人喜爱运动,其余不喜爱.
(1)根据以上数据完成以下![]() 列联表;并要求列联表的独立性检验,能否在犯错误的概率不超过
列联表;并要求列联表的独立性检验,能否在犯错误的概率不超过![]() 的前提下认为性别与喜爱运动有关?
的前提下认为性别与喜爱运动有关?
喜爱运动 | 不喜爱运动 | 总计 | |
男 |
|
| |
女 |
|
| |
总计 |
|
(2)如果从喜欢运动的女志愿者中(其中恰有![]() 人会外语),抽取
人会外语),抽取![]() 名负责翻译工作,则抽出的志愿者中
名负责翻译工作,则抽出的志愿者中![]() 人恰有一人胜任翻译工作的概率是多少?
人恰有一人胜任翻译工作的概率是多少?
参考公式: ,其中
,其中![]() .
.
参考答数:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在第十五次全国国民阅读调查中,某地区调查组获得一个容量为![]() 的样本,其中城镇居民
的样本,其中城镇居民![]() 人,农村居民
人,农村居民![]() 人.在这些居民中,经常阅读的城镇居民
人.在这些居民中,经常阅读的城镇居民![]() 人,农村居民
人,农村居民![]() 人.
人.
(1)填写下面列联表,并判断是否有![]() 的把握认为,经常阅读与居民居住地有关?
的把握认为,经常阅读与居民居住地有关?
城镇居民 | 农村居民 | 合计 | |
经常阅读 |
|
| |
不经常阅读 | |||
合计 |
|
(2)调查组从该样本的城镇居民中按分层抽样抽取出![]() 人,参加一次阅读交流活动,若活动主办方从这
人,参加一次阅读交流活动,若活动主办方从这![]() 位居民中随机选取
位居民中随机选取![]() 人作交流发言,求被选中的
人作交流发言,求被选中的![]() 位居民都是经常阅读居民的概率.
位居民都是经常阅读居民的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() .
.
(1)若函数![]() 在
在![]() 上是增函数,求正数
上是增函数,求正数![]() 的取值范围;
的取值范围;
(2)当![]() 时,设函数
时,设函数![]() 的图象与x轴的交点为
的图象与x轴的交点为![]() ,
,![]() ,曲线
,曲线![]() 在
在![]() ,
,![]() 两点处的切线斜率分别为
两点处的切线斜率分别为![]() ,
,![]() ,求证:
,求证:![]() +
+![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为1的正方形,MD⊥ABCD,NB⊥ABCD.且MD=NB=1.则下列结论中:
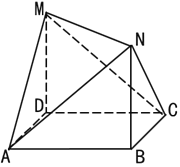
①MC⊥AN
②DB∥平面AMN
③平面CMN⊥平面AMN
④平面DCM∥平面ABN
所有假命题的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程是
的参数方程是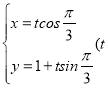 为参数),曲线
为参数),曲线![]() 的参数方程是
的参数方程是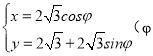 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求直线![]() 和曲线
和曲线![]() 的极坐标方程;
的极坐标方程;
(2)已知射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,射线
两点,射线![]() 与直线
与直线![]() 交于
交于![]() 点,若
点,若![]() 的面积为1,求
的面积为1,求![]() 的值和弦长
的值和弦长![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
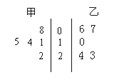
【题目】某校高中年级开设了丰富多彩的校本课程,甲、乙两班各随机抽取了5名学生的学分,用茎叶图表示.![]() ,
,![]() 分别表示甲、乙两班各自5名学生学分的标准差,则
分别表示甲、乙两班各自5名学生学分的标准差,则![]() _______
_______![]() .(填“
.(填“![]() ”“<”或“=”)
”“<”或“=”)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且曲线
,且曲线![]() 与
与![]() 恰有一个公共点.
恰有一个公共点.
(Ⅰ)求曲线![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)已知曲线![]() 上两点
上两点![]() ,
,![]() 满足
满足![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com