Question

【题目】已知椭圆C的标准方程为：，该椭圆经过点P（1，），且离心率为．

（Ⅰ）求椭圆的标准方程；

（Ⅱ）过椭圆长轴上一点S（1，0）作两条互相垂直的弦AB、CD．若弦AB、CD的中点分别为M、N，证明：直线MN恒过定点．

Answer 1

【答案】（1）（2）

【解析】

（Ⅰ）由已知条件推导出，e=，由此能求出椭圆方程．

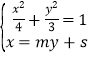（Ⅱ）设直线AB的方程为x=my+s，m≠0，则直线CD的方程为x=﹣，联立，得M（），将M的坐标中的m用﹣代换，得CD的中点N（），从而得到直线MN的方程为x﹣y=，由此能证明直线MN经过定点（）．

（Ⅰ）解：∵点P（1，）在椭圆上，∴，又∵离心率为，∴e=，∴a=2c，∴4a2﹣4b2=a2，解得a2=4，b2=3，

∴椭圆方程为．

（Ⅱ）证明：设直线AB的方程为x=my+s，m≠0，则直线CD的方程为x=﹣，联立，得（3m2+4）y2+6smy+3s2﹣12=0，

设A（x1，y1），B（x2，y2），则，，∴x1+x2=（my1+s）（my2+s）=m2y1y2+ms（y1+y2）+s2=，

由中点坐标公式得M（，﹣），将M的坐标中的m用﹣代换，得CD的中点N（，）

∴直线MN的方程为x﹣y=，m≠±1，令y=0得：x=，∴直线MN经过定点（），

当m=0，±1时，直线MN也经过定点（），综上所述，直线MN经过定点（）．

当时，过定点