
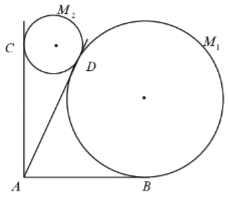
【题目】某景区欲建两条圆形观景步道![]() (宽度忽略不计),如图所示,已知
(宽度忽略不计),如图所示,已知![]() ,
,![]() (单位:米),要求圆M与
(单位:米),要求圆M与![]() 分别相切于点B,D,圆
分别相切于点B,D,圆![]() 与
与![]() 分别相切于点C,D.
分别相切于点C,D.
(1)若![]() ,求圆
,求圆![]() 的半径;(结果精确到0.1米)
的半径;(结果精确到0.1米)
(2)若观景步道![]() 的造价分别为每米0.8千元与每米0.9千元,则当
的造价分别为每米0.8千元与每米0.9千元,则当![]() 多大时,总造价最低?最低总造价是多少?(结果分别精确到0.1°和0.1千元)
多大时,总造价最低?最低总造价是多少?(结果分别精确到0.1°和0.1千元)
【答案】(1)34.6米,16.1米;(2)263.8千元.
【解析】
(1)利用切线的性质即可得出圆的半径;
(2)设∠BAD=2α,则总造价y=0.82π60tanα+0.92π60tan(45°﹣α),化简,令1+tanα=x换元,利用基本不等式得出最值.
(1)连结M1M2,AM1,AM2,
∵圆M1与AB,AD相切于B,D,圆M2与AC,AD分别相切于点C,D,
∴M1,M2⊥AD,∠M1AD=![]() ∠BAD=
∠BAD=![]() ,∠M2AD=
,∠M2AD=![]() ,
,
∴M1B=ABtan∠M1AB=60×![]() =20
=20![]() ≈34.6(米),
≈34.6(米),
∵tan![]() =
=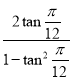 =
=![]() ,∴tan
,∴tan![]() =2﹣
=2﹣![]() ,
,
同理可得:M2D=60×tan![]() =60(2﹣
=60(2﹣![]() )≈16.1(米).
)≈16.1(米).
(2)设∠BAD=2α(0<α<![]() ),由(1)可知圆M1的半径为60tanα,圆M2的半径为
),由(1)可知圆M1的半径为60tanα,圆M2的半径为
60tan(45°﹣α),
设观景步道总造价为y千元,则y=0.82π60tanα+0.92π60tan(45°﹣α)=96πtanα+108π![]() ,
,
设1+tanα=x,则tanα=x﹣1,且1<x<2.
∴y=96π(x﹣1)+108π(![]() )=12π(8x+
)=12π(8x+![]() ﹣17)≥84π≈263.8,
﹣17)≥84π≈263.8,
当且仅当8x=![]() 即x=
即x=![]() 时取等号,
时取等号,
当x=![]() 时,tanα=
时,tanα=![]() ,∴α≈26.6°,2α≈53.2°.
,∴α≈26.6°,2α≈53.2°.
∴当∠BAD为53.2°时,观景步道造价最低,最低造价为263.8千元.


科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 上任意一点,
上任意一点,![]() ,且点
,且点![]() 为线段
为线段![]() 的中点.
的中点.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)若![]() 为点
为点![]() 关于原点
关于原点![]() 的对称点,过
的对称点,过![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 、
、![]() 两点,直线
两点,直线![]() 交直线
交直线![]() 于点
于点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() ),点
),点![]() 在
在![]() 的焦点
的焦点![]() 的右侧,且
的右侧,且![]() 到
到![]() 的准线的距离是
的准线的距离是![]() 到
到![]() 距离的3倍,经过点
距离的3倍,经过点![]() 的直线与抛物线
的直线与抛物线![]() 交于不同的
交于不同的![]() 、
、![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,经过点
,经过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求抛物线![]() 的方程和
的方程和![]() 的坐标;
的坐标;
(2)判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)椭圆![]() 的两焦点为
的两焦点为![]() 、
、![]() ,在椭圆
,在椭圆![]() 外的抛物线
外的抛物线![]() 上取一点
上取一点![]() ,若
,若![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln![]() +ax﹣1(a≠0).
+ax﹣1(a≠0).
(I)求函数f(x)的单调区间;
(Ⅱ)已知g(x)+xf(x)=﹣x,若函数g(x)有两个极值点x1,x2(x1<x2),求证:g(x1)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
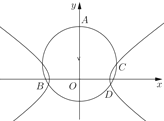
【题目】如图,已知圆![]() :
:![]() (
(![]() )和双曲线
)和双曲线![]() :
:![]() (
(![]() ),记
),记![]() 与
与![]() 轴正半轴、
轴正半轴、![]() 轴负半轴的公共点分别为
轴负半轴的公共点分别为![]() 、
、![]() ,又记
,又记![]() 与
与![]() 在第一、第四象限的公共点分别为
在第一、第四象限的公共点分别为![]() 、
、![]() .
.
(1)若![]() ,且
,且![]() 恰为
恰为![]() 的左焦点,求
的左焦点,求![]() 的两条渐近线的方程;
的两条渐近线的方程;
(2)若![]() ,且
,且![]() ,求实数
,求实数![]() 的值;
的值;
(3)若![]() 恰为
恰为![]() 的左焦点,求证:在
的左焦点,求证:在![]() 轴上不存在这样的点
轴上不存在这样的点![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆:![]() 的左、右点分别为
的左、右点分别为![]() 点
点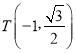 在椭圆上,且
在椭圆上,且![]()
(1)求椭圆![]() 的方程;
的方程;
(2)过点(1,0)作斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于M、N两点,若
于M、N两点,若![]() 求直线
求直线![]() 的方程;
的方程;
(3)点P、Q为椭圆上的两个动点,![]() 为坐标原点,若直线
为坐标原点,若直线![]() 的斜率之积为
的斜率之积为![]() 求证:
求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果数列![]() 对于任意
对于任意![]() ,都有
,都有![]() ,其中
,其中![]() 为常数,则称数列
为常数,则称数列![]() 是“间等差数列”,
是“间等差数列”,![]() 为“间公差”.若数列
为“间公差”.若数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)求证:数列![]() 是“间等差数列”,并求间公差
是“间等差数列”,并求间公差![]() ;
;
(2)设![]() 为数列
为数列![]() 的前n项和,若
的前n项和,若![]() 的最小值为-153,求实数
的最小值为-153,求实数![]() 的取值范围;
的取值范围;
(3)类似地:非零数列![]() 对于任意
对于任意![]() ,都有
,都有![]() ,其中
,其中![]() 为常数,则称数列
为常数,则称数列![]() 是“间等比数列”,
是“间等比数列”,![]() 为“间公比”.已知数列
为“间公比”.已知数列![]() 中,满足
中,满足![]() ,
,![]() ,
,![]() ,试问数列
,试问数列![]() 是否为“间等比数列”,若是,求最大的整数
是否为“间等比数列”,若是,求最大的整数![]() 使得对于任意
使得对于任意![]() ,都有
,都有![]() ;若不是,说明理由.
;若不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com