
【题目】“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手大多在以下两个年龄段:21~30,31~40(单位:岁),统计这两个年龄段选手答对歌曲名称与否的人数如图所示.
(参考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
(1)写出2×2列联表,并判断是否有90%的把握认为答对歌曲名称与否和年龄有关,说明你的理由.(下面的临界值表供参考)
P(K2≥k0) | 0.1 | 0.05 | 0.01 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
(2)在统计过的参考选手中按年龄段分层选取9名选手,并抽取3名幸运选手,求3名幸运选手中在21~30岁年龄段的人数的分布列和数学期望.
【答案】
(1)解:2×2列联表
正确 | 错误 | 合计 | |
21~30 | 10 | 30 | 40 |
31~40 | 10 | 70 | 80 |
合计 | 20 | 100 | 120 |
∴K2= ![]() =3>2.706
=3>2.706
有90%的把握认为猜对歌曲名称与否和年龄有关
(2)解:按照分层抽样方法可知:21~30(岁)抽取3人,31~40(岁)抽取6人.
设3名选手中在21~30岁之间的人数为ξ,可能取值为0,1,2,3
P(ξ=0)= ![]() =
= ![]() ,P(ξ=1)=
,P(ξ=1)= ![]() =
= ![]() ,P(ξ=2)=
,P(ξ=2)= ![]() =
= ![]() ,P(ξ=3)=
,P(ξ=3)= ![]() =
= ![]() .
.
ξD的分布列
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
E(ξ)=0× ![]() +1×
+1× ![]() +2×
+2× ![]() +3×
+3× ![]() =1
=1
【解析】(1)根据所给的二维条形图得到列联表,利用公式求出k2=3>2.706,即可得出结论.(2)设3名选手中在20~30岁之间的人数为ξ,可能取值为0,1,2,3,求出概率,列出分布列,求解期望即可.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD的底面ABCD为菱形,且∠ABC=60°,
AB=PC=2,PA=PB= ![]() .
.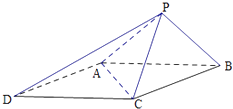
(1)求证:平面PAB⊥平面ABCD;
(2)设H是PB上的动点,求CH与平面PAB所成最大角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,且f(α)=1,α∈(0, ![]() ),则cos(2
),则cos(2 ![]() )=( )
)=( )
A.![]()
B.![]()
C.﹣ ![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(xy)=f(x)+f(y).
(1) 若x,y∈R,求f(1),f(-1)的值; (2)若x,y∈R,判断y=f(x)的奇偶性;
(3)若函数f(x)在其定义域(0,+∞)上是增函数,f(2)=1,f(x)+f(x-2)≤3,求x的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ex﹣lnx.
(参考数据:e≈2.718,ln2≈0.693,ln3≈1.099,ln5≈1.609,ln7≈1.946)
(1)求证:函数f(x)有且只有一个极值点x0;
(2)求函数f(x)的极值点x0的近似值x′,使得|x′﹣x0|<0.1;
(3)求证:f(x)>2.3对x∈(0,+∞)恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市“招手即停”公共汽车的票价按下列规则制定:
5公里以内(含5公里),票价2元;
5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算).如果某条线路的总里程为20公里,请根据题意.
(1)写出票价与里程之间的函数解析式;
(2)根据(1)写出的函数解析式试画出该函数的图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱猪ABCD﹣A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,A1A=AB=2,E为棱AA1的中点.
(1)证明:B1C1⊥CE;
(2)求二面角B1﹣CE﹣C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ( x R ,且 e 为自然对数的底数).
( x R ,且 e 为自然对数的底数).
⑴ 判断函数 f x 的单调性与奇偶性;
⑵是否存在实数 t ,使不等式![]() 对一切的 x R 都成立?若存在,求出 t 的值,若 不存在说明理由.
对一切的 x R 都成立?若存在,求出 t 的值,若 不存在说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com