
已知函数 .
.
(1)求 在
在 上的最大值;
上的最大值;
(2)若直线 为曲线
为曲线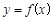 的切线,求实数
的切线,求实数 的值;
的值;
(3)当 时,设
时,设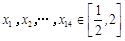 ,且
,且 ,若不等式
,若不等式 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.
(1)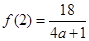 (2)
(2)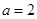 或
或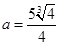 . (3)
. (3) 的最小值为
的最小值为 .
.
解析试题分析:
(1)利用导数可以求解函数单调性得到极值与最值,但是函数含有参数,故而需要讨论,首先对函数求定义域,求导可以发现导函数的分母恒大于0不影响导函数符号,故考虑分子大于0,小于0的解集,讨论a的范围得到区间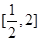 的单调性,分析就可以得到原函数在固定区间上的最值.
的单调性,分析就可以得到原函数在固定区间上的最值.
(2)设出切点坐标,利用切点满足的三个条件(①切点在原函数上,坐标满足原函数方程 ②切点在切线上,坐标满足切线方程 ③原函数在切点处的导数为切线的斜率)建立关于a的方程,解方程求出a的值.
(3)由(2)的结论得到此时直线 为曲线
为曲线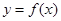 的切线,且分析原函数与切线的图像可以发现曲线
的切线,且分析原函数与切线的图像可以发现曲线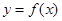 在直线
在直线 下方,即可以发现在区间
下方,即可以发现在区间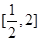 上不等式
上不等式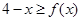 恒成立,作差即可严格证明该不等式是成立的.利用该不等式对
恒成立,作差即可严格证明该不等式是成立的.利用该不等式对 放缩为可求和的式子,进而求的
放缩为可求和的式子,进而求的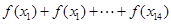 的最值,得到
的最值,得到 的取值范围与最值.
的取值范围与最值.
试题解析:
(1)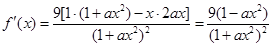 , 2分
, 2分
令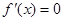 ,解得
,解得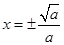 (负值舍去),
(负值舍去),
由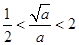 ,解得
,解得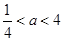 .
.
(ⅰ)当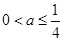 时,由
时,由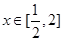 ,得
,得 ,
,
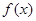 在
在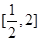 上的最大值为
上的最大值为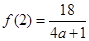 . 3分
. 3分
(ⅱ)当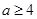 时,由
时,由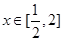 ,得
,得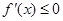 ,
,
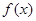 在
在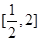 上的最大值为
上的最大值为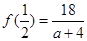 . 4分
. 4分
(ⅲ)当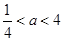 时,
时, 在
在 时,
时,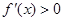 ,在
,在 时,
时, ,
,
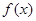 在
在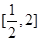 上的最大值为
上的最大值为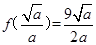 . 5分
. 5分
(2)设切点为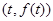 ,则
,则 6分
6分
由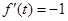 ,有
,有 ,化简得
,化简得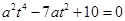 ,
,
即 或
或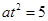 , ①
, ①
由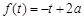 ,有
,有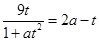 ,②
,②
由①、②解得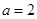 或
或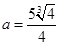 . 9分
. 9分
(3)当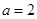 时,
时,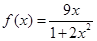 ,
,
由(2)的结论直线 为曲线
为曲线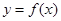 的切线,
的切线,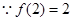 ,
, 点
点 在直线
在直线 上,
上,
根据图像分析,曲线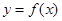 在直线
在直线 下方. 10分
下方. 10分
下面给出证明:当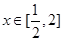 时,
时,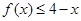 .
.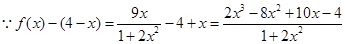


科目:高中数学 来源: 题型:解答题
请你设计一个包装盒,如图所示,ABCD是边长为60 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E,F在AB上,是被切去的一个等腰直角三角形,斜边的两个端点,设AE=FB=x(cm).
①某广告商要求包装盒的侧面积S(cm2)最大,试问x应取何值?
②某厂商要求包装盒的容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设f(x)=- x3+
x3+ x2+2ax.
x2+2ax.
(1)若f(x)在( ,+∞)上存在单调递增区间,求a的取值范围.
,+∞)上存在单调递增区间,求a的取值范围.
(2)当0<a<2时,f(x)在[1,4]上的最小值为- ,求f(x)在该区间上的最大值.
,求f(x)在该区间上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设f(x)=ln(x2+1),g(x)= x2-
x2- .
.
(1)求F(x)=f(x)-g(x)的单调区间,并证明对[-1,1]上的任意x1,x2,x3,都有F(x1)+F(x2)>F(x3);
(2)将y=f(x)的图像向下平移a(a>0)个单位,同时将y=g(x)的图像向上平移b(b>0)个单位,使它们恰有四个交点,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ;
;
(1)若 >0,试判断f(x)在定义域内的单调性;
>0,试判断f(x)在定义域内的单调性;
(2)若f(x)在[1,e]上的最小值为 ,求
,求 的值;
的值;
(3)若f(x)<x2在(1, 上恒成立,求a的取值范围.
上恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,
, ,
, 图象与
图象与 轴异于原点的交点M处的切线为
轴异于原点的交点M处的切线为 ,
, 与
与 轴的交点N处的切线为
轴的交点N处的切线为 , 并且
, 并且 与
与 平行.
平行.
(1)求 的值;
的值;
(2)已知实数t∈R,求 的取值范围及函数
的取值范围及函数 的最小值;
的最小值;
(3)令 ,给定
,给定 ,对于两个大于1的正数
,对于两个大于1的正数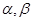 ,存在实数
,存在实数 满足:
满足: ,
, ,并且使得不等式
,并且使得不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式y= +10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
+10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
(1)求a的值;
(2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com