
【题目】已知一个几何体的三视图如下图,大致画出它的直观图,并求出它的表面积和体积.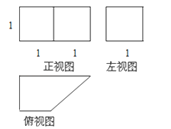
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() 过圆上任意一点
过圆上任意一点![]() 向
向![]() 轴引垂线垂足为
轴引垂线垂足为![]() (点
(点![]() 、
、![]() 可重合),点
可重合),点![]() 为
为![]() 的中点.
的中点.
(1)求![]() 的轨迹方程;
的轨迹方程;
(2)若点![]() 的轨迹方程为曲线
的轨迹方程为曲线![]() ,不过原点
,不过原点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,满足直线
两点,满足直线![]() ,
, ![]() ,
, ![]() 的斜率依次成等比数列,求
的斜率依次成等比数列,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】酒后违法驾驶机动车危害巨大,假设驾驶人员血液中的酒精含量为![]() (简称血酒含量,单位是毫克/100毫升),当
(简称血酒含量,单位是毫克/100毫升),当![]() 时,为酒后驾车;当
时,为酒后驾车;当![]() 时,为醉酒驾车.如图为某市交管部分在一次夜间行动中依法查出的
时,为醉酒驾车.如图为某市交管部分在一次夜间行动中依法查出的![]() 名饮酒后违法驾驶机动车者抽血检测后所得频率分布直方图(其中
名饮酒后违法驾驶机动车者抽血检测后所得频率分布直方图(其中![]() 人数包含
人数包含![]() ).
).
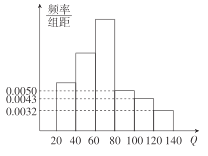
(Ⅰ)求查获的醉酒驾车的人数;
(Ⅱ)从违法驾车的![]() 人中按酒后驾车和醉酒驾车利用分层抽样抽取
人中按酒后驾车和醉酒驾车利用分层抽样抽取![]() 人做样本进行研究,再从抽取的
人做样本进行研究,再从抽取的![]() 人中任取
人中任取![]() 人,求
人,求![]() 人中含有醉酒驾车人数
人中含有醉酒驾车人数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 (本小题满分12分)
如图, 在四面体ABOC中, ![]() , 且
, 且![]() .
.
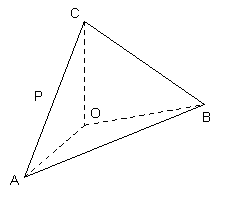
(Ⅰ)设为![]() 为
为![]() 的中点, 证明: 在
的中点, 证明: 在![]() 上存在一点
上存在一点![]() ,使
,使![]() ,并计算
,并计算![]() ;
;
(Ⅱ)求二面角![]() 的平面角的余弦值。
的平面角的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() ,定义
,定义![]() 为数列
为数列![]() 的一阶差分数列,其中
的一阶差分数列,其中![]() ,(
,( ![]() ),设
),设![]()
(1)若![]() ,求证:
,求证: ![]() 是等比数列,并求出
是等比数列,并求出![]() 的通项公式;
的通项公式;
(2)若![]() ,又数列
,又数列![]() 满足:
满足: ![]() :
:
①求数列![]() 的前
的前![]() 和
和![]() ;
;
②求证:数列![]() 中的任意一项总可以表示成该数列中其他两项之积.
中的任意一项总可以表示成该数列中其他两项之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
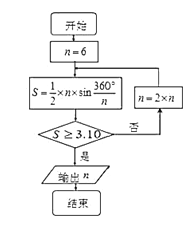
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值![]() ,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出
,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出![]() 的值为 ( )
的值为 ( )
(参考数据:![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
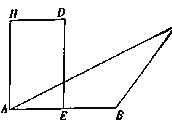
【题目】如图,在![]() 中,
中, ![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 垂直平分线上的一点,且
垂直平分线上的一点,且![]() ,四边形
,四边形![]() 为矩形,固定边
为矩形,固定边![]() ,在平面
,在平面![]() 内移动顶点
内移动顶点![]() ,使得
,使得![]() 的内切圆始终与
的内切圆始终与![]() 切于线段
切于线段![]() 的中点,且
的中点,且![]() 在直线
在直线![]() 的同侧,在移动过程中,当
的同侧,在移动过程中,当![]() 取得最小值时,点
取得最小值时,点![]() 到直线
到直线![]() 的距离为__________.
的距离为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() , 则下列关于函数y=f[f(x)]+1的零点个数的判断正确的是( )
, 则下列关于函数y=f[f(x)]+1的零点个数的判断正确的是( )
A.当k>0时,有3个零点;当k<0时,有2个零点
B.当k>0时,有4个零点;当k<0时,有1个零点
C.无论k为何值,均有2个零点
D.无论k为何值,均有4个零点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com