
【题目】已知椭圆![]() (
(![]() )的离心率是
)的离心率是![]() ,过点
,过点![]() 的动直线与椭圆相交于
的动直线与椭圆相交于![]() ,
, ![]() 两点,当直线
两点,当直线![]() 平行于
平行于![]() 轴时,直线
轴时,直线![]() 被椭圆截得的线段长为
被椭圆截得的线段长为![]() .
.
(1)求椭圆的方程;
(2)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)记椭圆的右顶点为![]() ,点
,点![]() (
(![]() )在椭圆上,直线
)在椭圆上,直线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 交
交![]() 轴于点
轴于点![]() .问:
.问: ![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() (
(![]() 为坐标原点)?若存在,求点
为坐标原点)?若存在,求点![]() 坐标;若不存在,说明理由.
坐标;若不存在,说明理由.
【答案】(1)![]() (2)
(2)![]() (3)点
(3)点![]() 的坐标为
的坐标为![]() 或
或![]()
【解析】试题分析:
(1)由题意求得![]() 则椭圆的方程为
则椭圆的方程为![]() ;
;
(2)很明显直线的斜率存在,利用弦长公式得到关于斜率k的方程,解方程可得![]() 的方程为
的方程为![]() .
.
(3) 假设![]() 轴上存在点
轴上存在点![]() ,使得
,使得![]() ,原问题等价于
,原问题等价于![]() 满足
满足![]() ,据此整理计算可得点
,据此整理计算可得点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
试题解析:
解:(1)由已知,点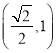 在椭圆上,
在椭圆上,
因此 解得
解得![]()
所以椭圆的方程为![]() .
.
(2)依题意,直线![]() 的斜率必存在,设
的斜率必存在,设![]() 的方程为
的方程为![]() ,
, ![]() ,
, ![]() ,
,
则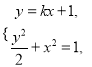
![]() ,
,
故![]() ,
, ![]() ,
,
∴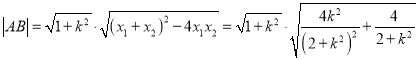
![]() ,
,
整理得![]() ,即
,即![]() ,
,
∴![]() 的方程为
的方程为![]() .
.
(3)假设![]() 轴上存在点
轴上存在点![]() ,使得
,使得![]() ,
,
“存在点![]() 使得
使得![]() ”等价于“存在点
”等价于“存在点![]() 使得
使得![]() ”
”
即![]() 满足
满足![]() ,
,
因为![]() ,所以
,所以![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
所以![]() ,即
,即![]() ,
,
因为点![]() 与点
与点![]() 关于
关于![]() 轴对称,所以
轴对称,所以![]() .
.
同理可得![]() ,
,
因为![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,
,
所以![]() 或
或![]() ,
,
故在![]() 轴上存在点
轴上存在点![]() ,使得
,使得![]() ,点
,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2﹣ax+3,且对任意的实数x都有f(4﹣x)=f(x)成立.
(1)求实数a的值;
(2)求函数f(x)在区间[0,3]上的值域;
(3)要得到函数y=x2的图象只需要将二次函数y=f(x)的图象做怎样的变换得到.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足f(x+1)﹣f(x)=2x(x∈R),且f(0)=1,
(1)求f(x)的解析式;
(2)当x∈[﹣1,1]时,求函数g(x)=f(x)﹣2x的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣x+2a﹣1(a>0).
(1)若f(x)在区间[1,2]为单调增函数,求a的取值范围;
(2)设函数f(x)在区间[1,2]上的最小值为g(a),求g(a)的表达式;
(3)设函数 ![]() ,若对任意x1 , x2∈[1,2],不等式f(x1)≥h(x2)恒成立,求实数a的取值范围.
,若对任意x1 , x2∈[1,2],不等式f(x1)≥h(x2)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】销售甲、乙两种商品所得利润分别是P(单位:万元)和Q(单位:万元),它们与投入资金t(单位:万元)的关系有经验公式P= ![]() t,Q=
t,Q= ![]() .今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资x(单位:万元),
.今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资x(单位:万元),
(1)试建立总利润y(单位:万元)关于x的函数关系式;
(2)当对甲种商品投资x(单位:万元)为多少时?总利润y(单位:万元)值最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x| ![]() >0},集合B={x|y=lg(﹣x2+3x+28)},集合C={x|m+1≤x≤2m﹣1}.
>0},集合B={x|y=lg(﹣x2+3x+28)},集合C={x|m+1≤x≤2m﹣1}.
(1)求(RA)∩B;
(2)若B∪C=B,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 与
与![]() 有相同的极值点.
有相同的极值点.
(I)求函数![]() 的解析式;
的解析式;
(II)证明:不等式![]() (其中e为自然对数的底数);
(其中e为自然对数的底数);
(III)不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com