
已知复数 是纯虚数。 (1)求
是纯虚数。 (1)求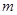 的值;
的值;
(2)若复数 ,满足
,满足 ,求
,求 的最大值。
的最大值。
解答:(1)方法一: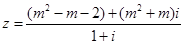
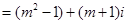 ……3分
……3分
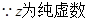
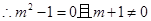
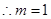 …………………………7分
…………………………7分
方法二: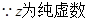
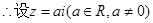
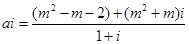
即 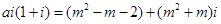 ………………………3分
………………………3分
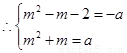 解得
解得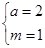 ……………………7分
……………………7分
(2)由(1)知,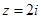 设
设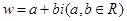
由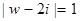 ,得:
,得: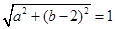 即
即 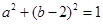 (*)………10分
(*)………10分
所以 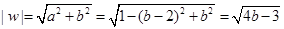 ,
………12分
,
………12分
由(*)得: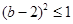 ,即
,即
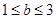 ,
,
所以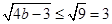 ,所以
,所以
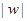 的最大值为3。………14分
的最大值为3。………14分
或 直接由式子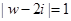 得复数
得复数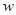 的几何意义是以(0,2)为圆心,1为半径的圆,
的几何意义是以(0,2)为圆心,1为半径的圆,
此圆上的点到原点的距离的最大值是3,所以 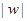 的最大值是3。………………14分
的最大值是3。………………14分
【解析】本试题主要是考查了复数的概念和复数的基本运算,以复数的几何意义的运用。
(1)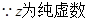
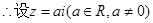
那么可知代入已知关系式中,得到复数相等,对应实部和虚部相等得到结论。
(2)由(1)知,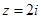 设
设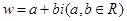 ,那么利用复数的几何意义,表示两点之间的距离,因为求解的是动点到定点的距离的最大值问题。
,那么利用复数的几何意义,表示两点之间的距离,因为求解的是动点到定点的距离的最大值问题。


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com