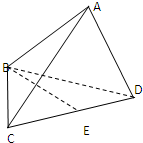
试题分析:(1)设AC交BD于O,以

、

、

分别为S

,D

,C

,
x轴、y轴、z轴的正方向,建立空间直角坐标系,则S

,D

,C

,
求出

,

的坐标,并计算得到

·

=0,从而AC⊥SD.(2)

为平面PAC的一个法向量,

为平面DAC的一个法向量,向量

与

的夹角等于二面角P

AC

D的平面角,根据向量的夹角公式计算出

与

的夹角即可.(3)假设存在一点E使BE∥平面PAC,设

=t

(0≤t≤1),则

=

+

=

+t

,因为

·

=0,可建立关于t的等式,解之即可.
试题解析:(1)证明:连接BD,设AC交BD于O,
由题意知SO⊥平面ABCD,以O为坐标原点,

、

、

分别为
x轴、y轴、z轴的正方向,建立空间直角坐标系.

设底面边长为a,,则高SO=

a.于是S

,D

,C

,

=

,

=

,

·

=0,故OC⊥SD,从而AC⊥SD. 4分
(2)解:由题设知,平面PAC的一个法向量为

=

,
平面DAC的一个法向量为

=

,则cos<

,

>=

=

,
故所求二面角的大小为30°. 8分
(3)解:在棱SC上存在一点E使BE∥平面PAC.,由(2)知

是平面PAC的一个法向量,
且

=

,

=

, 设

=t

(0≤t≤1),

=

+

=

+t

=

,而

·

=0

t=

,
即当SE∶EC=2∶1时,BE∥平面PAC. 12分

 ABCD的底面是正方形,每条侧棱的长都是底面边长的
ABCD的底面是正方形,每条侧棱的长都是底面边长的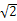 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.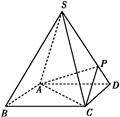
 AC
AC D的大小;
D的大小; 、
、 、
、 分别为S
分别为S ,D
,D ,C
,C ,
, ,D
,D ,C
,C ,
, ,
, 的坐标,并计算得到
的坐标,并计算得到 ·
· =0,从而AC⊥SD.(2)
=0,从而AC⊥SD.(2) 为平面PAC的一个法向量,
为平面PAC的一个法向量,
 与
与 的夹角等于二面角P
的夹角等于二面角P AC
AC D的平面角,根据向量的夹角公式计算出
D的平面角,根据向量的夹角公式计算出 与
与 的夹角即可.(3)假设存在一点E使BE∥平面PAC,设
的夹角即可.(3)假设存在一点E使BE∥平面PAC,设 =t
=t (0≤t≤1),则
(0≤t≤1),则 =
= +
+ =
= +t
+t ,因为
,因为 ·
· =0,可建立关于t的等式,解之即可.
=0,可建立关于t的等式,解之即可. 、
、 、
、 分别为
分别为
 a.于是S
a.于是S ,D
,D ,C
,C ,
, =
= ,
, =
= ,
, ·
· =0,故OC⊥SD,从而AC⊥SD. 4分
=0,故OC⊥SD,从而AC⊥SD. 4分 =
= ,
, =
= ,则cos<
,则cos< ,
, >=
>= =
= ,
, 是平面PAC的一个法向量,
是平面PAC的一个法向量, =
= ,
, =
= , 设
, 设 =t
=t (0≤t≤1),
(0≤t≤1), =
= +
+ =
= +t
+t =
= ,而
,而 ·
· =0
=0 t=
t= ,
,

 名校课堂系列答案
名校课堂系列答案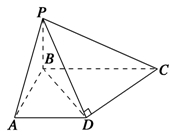
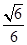 ?若存在,指出点E在棱PA上的位置,若不存在,说明理由.
?若存在,指出点E在棱PA上的位置,若不存在,说明理由.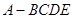 中,
中,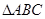 是正三角形,四边形
是正三角形,四边形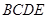 是矩形,且平面
是矩形,且平面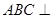 平面
平面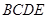 ,
,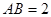 ,
,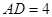 .
.
 是
是 的中点,求证:
的中点,求证: 平面
平面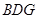 ;
;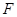 在线段
在线段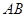 上什么位置时,二面角
上什么位置时,二面角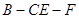 的余弦值为
的余弦值为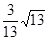 .
.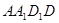 与矩形
与矩形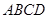 所在平面互相垂直,
所在平面互相垂直,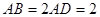 ,点
,点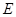 为
为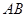 的中点.
的中点.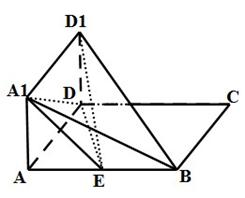
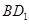 ∥平面
∥平面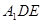 ;
;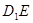
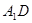 ;
;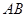 上是否存在点
上是否存在点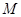 ,使二面角
,使二面角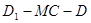 的大小为
的大小为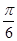 ?若存在,求出
?若存在,求出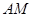 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.