
【题目】若实数数列![]() 满足
满足![]() ,则称数列
,则称数列![]() 为“
为“![]() 数列”.
数列”.
(Ⅰ)若数列![]() 是
是![]() 数列,且
数列,且![]() ,求
,求![]() ,
,![]() 的值;
的值;
(Ⅱ)求证:若数列![]() 是
是![]() 数列,则
数列,则![]() 的项不可能全是正数,也不可能全是负数;
的项不可能全是正数,也不可能全是负数;
(Ⅲ)若数列![]() 为
为![]() 数列,且
数列,且![]() 中不含值为零的项,记
中不含值为零的项,记![]() 前
前![]() 项中值为负数的项的个数为
项中值为负数的项的个数为![]() ,求
,求![]() 所有可能取值.
所有可能取值.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)见解析;(Ⅲ)
;(Ⅱ)见解析;(Ⅲ)![]() 的取值集合为
的取值集合为![]() .
.
【解析】
试题分析:(Ⅰ)由递推公式可得,![]()
![]() ,
,![]() ,再由
,再由![]() 可得
可得![]() ,
,![]() ,
,![]() ;(Ⅱ)此命题是否定性命题,可用反证法证明,即假设数列中各项全是正数(或全是负数),由递推公式推出矛盾即可;(Ⅲ)这类问题的数列应该是有一定的规律,最简单的就是周期数列,首先由(Ⅱ)可知
;(Ⅱ)此命题是否定性命题,可用反证法证明,即假设数列中各项全是正数(或全是负数),由递推公式推出矛盾即可;(Ⅲ)这类问题的数列应该是有一定的规律,最简单的就是周期数列,首先由(Ⅱ)可知![]() 数列
数列![]() 中项既有负数也有正数,
中项既有负数也有正数,
且最多连续两项都是负数,最多连续三项都是正数.因此存在最小的正整数![]() 满足
满足![]() (
(![]() ).设
).设![]() ,则由递推公式计算,最后可知数列是周期为9的周期数列,由刚才的计算可知在
,则由递推公式计算,最后可知数列是周期为9的周期数列,由刚才的计算可知在![]() 这9个数中有6个正数,3个负数,接着只要对
这9个数中有6个正数,3个负数,接着只要对![]() 分别讨论(关键是
分别讨论(关键是![]() 中有几个负数).
中有几个负数).
试题解析:(Ⅰ)因为![]() 是
是![]() 数列,且
数列,且![]()
所以![]() ,
,
所以![]() ,
,
所以![]() ,解得
,解得![]() ,
,
所以![]() .
.
(Ⅱ)假设![]() 数列
数列![]() 的项都是正数,即
的项都是正数,即![]() ,
,
所以![]() ,
,![]() ,与假设矛盾.
,与假设矛盾.
故![]() 数列
数列![]() 的项不可能全是正数,
的项不可能全是正数,
假设![]() 数列
数列![]() 的项都是负数,
的项都是负数,
则![]() 而
而![]() ,与假设矛盾,
,与假设矛盾,
故![]() 数列
数列![]() 的项不可能全是负数.
的项不可能全是负数.
(Ⅲ)由(Ⅱ)可知![]() 数列
数列![]() 中项既有负数也有正数,
中项既有负数也有正数,
且最多连续两项都是负数,最多连续三项都是正数.
因此存在最小的正整数![]() 满足
满足![]() (
(![]() ).
).
设![]() ,则
,则
![]() .
.
![]() ,
,
故有![]() , 即数列
, 即数列![]() 是周期为9的数列
是周期为9的数列
由上可知![]() 这9项中
这9项中![]() 为负数,
为负数,![]() 这两项中一个为正数,另一个为负数,其余项都是正数.
这两项中一个为正数,另一个为负数,其余项都是正数.
因为![]() ,
,
所以当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() 这
这![]() 项中至多有一项为负数,而且负数项只能是
项中至多有一项为负数,而且负数项只能是![]() ,
,
记![]() 这
这![]() 项中负数项的个数为
项中负数项的个数为![]() ,
,
当![]() 时,若
时,若![]() 则
则![]() ,故
,故![]() 为负数,
为负数,
此时![]() ,
,![]() ;
;
若![]() 则
则![]() ,故
,故![]() 为负数.
为负数.
此时![]() ,
,![]() ,
,
当![]() 时,
时,![]() 必须为负数,
必须为负数,![]() ,
,![]() ,
,
综上可知![]() 的取值集合为
的取值集合为![]() .
.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,已知曲线![]() ,将曲线
,将曲线![]() 上的点向左平移一个单位,然后纵坐标不变,横坐标轴伸长到原来的2倍,得到曲线
上的点向左平移一个单位,然后纵坐标不变,横坐标轴伸长到原来的2倍,得到曲线![]() ,又已知直线
,又已知直线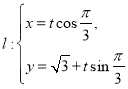 (
(![]() 是参数),且直线
是参数),且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(I)求曲线![]() 的直角坐标方程,并说明它是什么曲线;
的直角坐标方程,并说明它是什么曲线;
(II)设定点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
, ![]() 为棱
为棱![]() 中点.
中点. ![]() ,
, ![]() ,
, ![]() .
.

(I)求证: ![]() 平面
平面![]() .
.
(II)求证: ![]() 平面
平面![]() .
.
(III)在棱![]() 的上是否存在点
的上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?如果存在,求此时
?如果存在,求此时![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市拟兴建九座高架桥,新闻媒体对此进行了问卷调查,在所有参与调查的市民中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
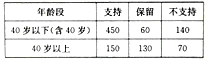
(1)在所有参与调查的人中,用分层抽样的方法抽取部分市民做进一步调研(不同态度的群体中亦按年龄分层抽样),已知从“保留”态度的人中抽取了19人,则在“支持”态度的群体中,年龄在40岁以下(含40岁)的人有多少被抽取;
(2)在持“不支持”态度的人中,用分层抽样的方法抽取6人做进一步的调研,将此6人看作一个总体,在这6人中任意选取2人,求至少有1人在40岁以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知有穷数列![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,若数列
,若数列![]() 中各项都是集合
中各项都是集合![]() 的元素,则称该数列为
的元素,则称该数列为![]() 数列.
数列.
对于![]() 数列
数列![]() ,定义如下操作过程
,定义如下操作过程![]() 从
从![]() 中任取两项
中任取两项![]() ,
, ![]() ,将
,将![]() 的值添在
的值添在![]() 的最后,然后删除
的最后,然后删除![]() ,
, ![]() ,这样得到一个
,这样得到一个![]() 项的新数列,记作
项的新数列,记作![]() (约定:一个数也视作数列).若
(约定:一个数也视作数列).若![]() 还是
还是![]() 数列,可继续实施操作过程
数列,可继续实施操作过程![]() .得到的新数列记作
.得到的新数列记作![]() ,
, ![]() ,如此经过
,如此经过![]() 次操作后得到的新数列记作
次操作后得到的新数列记作![]() .
.
(Ⅰ)设![]() ,
, ![]() ,
, ![]() ,
, ![]() ,请写出
,请写出![]() 的所有可能的结果.
的所有可能的结果.
(Ⅱ)求证:对![]() 数列
数列![]() 实施操作过程
实施操作过程![]() 后得到的数列
后得到的数列![]() 仍是
仍是![]() 数列.
数列.
(Ⅲ)设![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的所有可能的结果,并说明理由.
的所有可能的结果,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,过其右焦点
,过其右焦点![]() 与长轴垂直的直线与椭圆在第一象限相交于点
与长轴垂直的直线与椭圆在第一象限相交于点![]() ,
, ![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆![]() 的左顶点为
的左顶点为![]() ,右顶点为
,右顶点为![]() ,点
,点![]() 是椭圆上的动点,且点
是椭圆上的动点,且点![]() 与点
与点![]() ,
, ![]() 不重合,直线
不重合,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,求证:以线段
,求证:以线段![]() 为直径的圆恒过定点.
为直径的圆恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
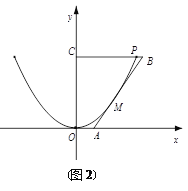
【题目】为响应新农村建设,某村计划对现有旧水渠进行改造,已知旧水渠的横断面是一段抛物线弧,顶点为水渠最底端(如图),渠宽为4m,渠深为2m.
(1)考虑到农村耕地面积的减少,为节约水资源,要减少水渠的过水量,在原水渠内填土,使其成为横断面为等腰梯形的新水渠(如图(1)建立平面直角坐标系),新水渠底面与地面平行(不改变渠宽),问新水渠底宽为多少时,所填土的土方量最少?
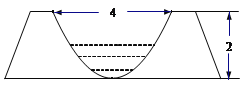
(2)考虑到新建果园的灌溉需求,要增大水渠的过水量,现把旧水渠改挖(不能填土)成横断面为等腰梯形的新水渠(如图(2)建立平面直角坐标系),使水渠的底面与地面平行(不改变渠深),要使所挖土的土方量最少,请你设计水渠改挖后的底宽,并求出这个底宽.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加其中一组.在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的![]() ,且该组中青年人占50%,中年人占40%,老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.试确定:
,且该组中青年人占50%,中年人占40%,老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.试确定:
(1)游泳组中,青年人、中年人、老年人分别所占的比例;
(2)游泳组中,青年人、中年人、老年人分别应抽取的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com