
【题目】在如图所示的空间几何体中,平面![]() 平面
平面![]() ,
,![]() 与
与![]() 都是边长为2的等边三角形,
都是边长为2的等边三角形,![]() ,
,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,且点E在平面
,且点E在平面![]() 上的射影落在
上的射影落在![]() 的平分线上.
的平分线上.
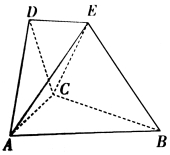
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,可证得
,可证得![]() 平面
平面![]() ,作
,作![]() 平面
平面![]() ,那么
,那么![]() ,通过证明四边形
,通过证明四边形![]() 是平行四边形,证得
是平行四边形,证得![]() ,由线面平行的判定定理证明;(2)以
,由线面平行的判定定理证明;(2)以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴的正方向建立空间直角坐标系,求出平面
轴的正方向建立空间直角坐标系,求出平面![]() 的一个法向量和平面
的一个法向量和平面![]() 的法向量的夹角,即得二面角
的法向量的夹角,即得二面角![]() 的余弦值.
的余弦值.
试题解析:(1)由题意知![]() 、
、![]() 为边长2的等边
为边长2的等边![]() 取
取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
则![]() ,
,![]() .又平面
.又平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,作
,作![]() 平面
平面![]() ,
,
那么![]() ,根据题意,点
,根据题意,点![]() 落在
落在![]() 上,
上,![]() 和平面
和平面![]() 所成的角为
所成的角为![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,![]() .
.
![]() 平面ABC,
平面ABC,![]() 平面
平面![]() ,
, ![]() 平面
平面![]() .
.
(2)建立空间直角坐标系![]() ,则
,则![]() ,
,![]() ,
,![]() ,
, ![]()
![]()
平面![]() 的一个法向量为
的一个法向量为![]()
设平面![]() 的法向量
的法向量![]() 则
则

取![]() ,
,![]()
![]() ,又由图知,所求二面角的平面角是锐角,二面角
,又由图知,所求二面角的平面角是锐角,二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知集合A={1,2,3,4,5,6,7,8,9),在集合A中任取三个元素,分别作为一个三位数的个位数,十位数和百位数,记这个三位数为a,现将组成a的三个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=219,则I(a)=129,D(a)=921),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,则输出b的值为( )
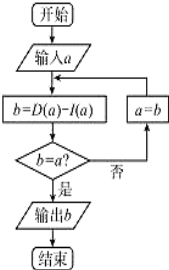
A.792 B.693
C.594 D.495
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨),一位居民的月用水量不超过
(吨),一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照![]() ,…,
,…,![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
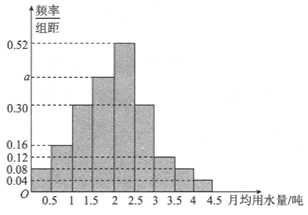
(1)求直方图中![]() 的值;
的值;
(2)若该市有110万居民,估计全市居民中月均用水量不低于3吨的人数,请说明理由;
(3)估计居民月均用水量的中位数(精确到0.01)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一批![]() 产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批
产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批![]() 产品所需原材料减少了
产品所需原材料减少了![]() 吨,且每吨原材料创造的利润提高了
吨,且每吨原材料创造的利润提高了![]() ;若将少用的
;若将少用的![]() 吨原材料全部用于生产公司新开发的
吨原材料全部用于生产公司新开发的![]() 产品,每吨原材料创造的利润为
产品,每吨原材料创造的利润为![]() 万元,其中a>0.
万元,其中a>0.
(1)若设备升级后生产这批A产品的利润不低于原来生产该批A产品的利润,求![]() 的取值范围;
的取值范围;
(2)若生产这批B产品的利润始终不高于设备升级后生产这批A产品的利润,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆的一组![]() 等分点分别涂上红色或蓝色,从任意一点开始,按逆时针方向依次记录
等分点分别涂上红色或蓝色,从任意一点开始,按逆时针方向依次记录![]() (
(![]() )个点的颜色,称为该圆的一个“
)个点的颜色,称为该圆的一个“![]() 阶色序”,当且仅当两个
阶色序”,当且仅当两个![]() 阶色序对应位置上的颜色至少有一个不相同时,称为不同的
阶色序对应位置上的颜色至少有一个不相同时,称为不同的![]() 阶色序.若某国的任意两个“
阶色序.若某国的任意两个“![]() 阶色序”均不相同,则称该圆为“
阶色序”均不相同,则称该圆为“![]() 阶魅力圆”.“3阶魅力圆”中最多可有的等分点个数为( )
阶魅力圆”.“3阶魅力圆”中最多可有的等分点个数为( )
A.4 B.6 C.8 D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(1)当![]() ,求函数
,求函数![]() 的单调递增区间;
的单调递增区间;
(2)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,若
,若![]() 在
在![]() 内恒成立,则称
内恒成立,则称![]() 为函数
为函数![]() 的“类对称点”,当
的“类对称点”,当![]() 时,试问
时,试问![]() 是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程x2+y2-2(m+3)x+2(1-4m2)y+16m4+9=0表示一个圆.
(1) 求实数m的取值范围;
(2) 求该圆半径r的取值范围;
(3) 求该圆心的纵坐标的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com