【题目】已知x∈（1，5），则函数y= 
+ 
的最小值为 ．
【答案】
【解析】解：函数的导数f′（x）= 
， 由f′（x）=0得x2﹣18x+49=0得x= 
= 
=9±4 
，
∵x∈（1，5），
∴x=9﹣4 ，
当1＜x＜9﹣4 时，f′（x）＜0，函数单调递减，
当9﹣4 ＜x＜5时，f′（x）＞0，函数单调递增，
故当x=9﹣4 时，函数f（x）取得极小值，同时也是最小值，此时f（9﹣4 ）= 
+ 
= 
= 
+ 
= ，
所以答案是：
【考点精析】本题主要考查了函数的最大(小)值与导数的相关知识点，需要掌握求函数
在
上的最大值与最小值的步骤：（1）求函数在
内的极值；（2）将函数的各极值与端点处的函数值
，
比较，其中最大的是一个最大值，最小的是最小值才能正确解答此题．
全能测控一本好卷系列答案科目：高中数学 来源： 题型：
【题目】在△ABC中，已知（a2+b2）sin（A﹣B）=（a2﹣b2）sin（A+B），则△ABC的形状（ ）
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知： 
、 
、 
是同一平面上的三个向量，其中 =（1，2）．
（1）若| |=2 
，且 ∥ ，求 的坐标．
（2）若| |= 
，且 +2 与2 ﹣ 垂直，求 与 的夹角θ
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知向量 
=（cosx，﹣1）， 
=（ 
sinx，cos2x），设函数f（x）= + 
．
（Ⅰ）求函数f（x）的最小正周期和单调递增区间；
（Ⅱ）当x∈（0， 
）时，求函数f（x）的值域．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，半径为1，圆心角为 
的圆弧 
上有一点C．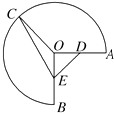 
（1）若C为圆弧AB的中点，点D在线段OA上运动，求| 
|的最小值；
（2）若D，E分别为线段OA，OB的中点，当C在圆弧 上运动时，求 
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在直三棱柱ABC﹣A1B1C1中，D，E分别为AB，BC的中点，点F在侧棱B1B上，且B1D⊥A1F，A1C1⊥A1B1 ． 求证：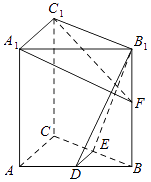 
（1）直线DE∥平面A1C1F；
（2）平面B1DE⊥平面A1C1F．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给定两个命题p：函数y=x2+8ax+1在[﹣1，1]上单调递增；q：方程 
=1表示双曲线，如果命题“p∧q”为假命题，“p∨q”为真命题，求实数a的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
