
已知![]() 的两个顶点
的两个顶点![]() 的坐标分别
的坐标分别![]() ,且
,且![]() 所在直线的斜率之积为
所在直线的斜率之积为![]() ,1)求顶点
,1)求顶点![]() 的轨迹.2)当
的轨迹.2)当![]() 时,记顶点
时,记顶点![]() 的轨迹为
的轨迹为![]() ,过点
,过点![]() 能否存在一条直线
能否存在一条直线![]() ,使
,使![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() 为线段
为线段![]() 的中点,若存在求直线
的中点,若存在求直线![]() 的方程,若不存在说明理由.(12分)
的方程,若不存在说明理由.(12分)
 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源:2010-2011年广东省广州市高二下学期期末教学质量检测理科数学 题型:解答题
(本小题满分12分)
已知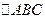 的两个顶点
的两个顶点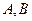 的坐标为
的坐标为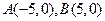 ,且
,且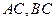 的斜率之积等于
的斜率之积等于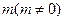 ,若顶点
,若顶点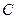 的轨迹是双曲线(去掉两个顶点),求
的轨迹是双曲线(去掉两个顶点),求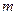 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省八市高三三月调考理科数学试卷(解析版) 题型:解答题
已知△ 的两个顶点
的两个顶点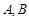 的坐标分别是
的坐标分别是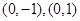 ,且
,且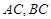 所在直线的斜率之积等于
所在直线的斜率之积等于 .
.
(Ⅰ)求顶点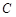 的轨迹
的轨迹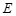 的方程,并判断轨迹
的方程,并判断轨迹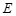 为何种圆锥曲线;
为何种圆锥曲线;
(Ⅱ)当 时,过点
时,过点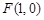 的直线
的直线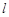 交曲线
交曲线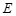 于
于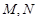 两点,设点
两点,设点 关于
关于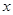 轴的对称
轴的对称
点为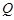 (
(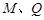 不重合) 试问:直线
不重合) 试问:直线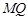 与
与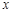 轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省八市高三3月联考理科数学试卷(解析版) 题型:解答题
(本题满分13分)已知△ 的两个顶点
的两个顶点 的坐标分别是
的坐标分别是 ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于 .
.
(Ⅰ)求顶点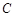 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 为何种圆锥曲线;
为何种圆锥曲线;
(Ⅱ)当 时,过点
时,过点 的直线
的直线 交曲线
交曲线 于
于 两点,设点
两点,设点 关于
关于 轴的对称点为
轴的对称点为 (
( 不重合) 试问:直线
不重合) 试问:直线 与
与 轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2010年黑龙江省高二上学期期中考试数学理卷 题型:解答题
已知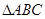 的两个顶点
的两个顶点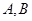 的坐标分别
的坐标分别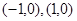 ,且
,且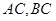 所在直线的斜率之积为
所在直线的斜率之积为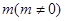 ,1)求顶点
,1)求顶点 的轨迹.2)当
的轨迹.2)当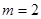 时,记顶点
时,记顶点 的轨迹为
的轨迹为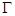 ,过点
,过点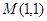 能否存在一条直线
能否存在一条直线 ,使
,使 与曲线
与曲线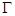 交于
交于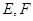 两点,且
两点,且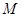 为线段
为线段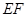 的中点,若存在求直线
的中点,若存在求直线 的方程,若不存在说明理由.(12分)
的方程,若不存在说明理由.(12分)
查看答案和解析>>
科目:高中数学 来源:2010年山西省高一上学期期中考试数学试卷 题型:解答题
已知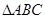 的两个顶点
的两个顶点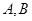 的坐标分别
的坐标分别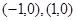 ,且
,且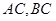 所在直线的斜率之积为
所在直线的斜率之积为 ,1)求顶点
,1)求顶点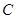 的轨迹.2)当
的轨迹.2)当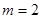 时,记顶点
时,记顶点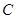 的轨迹为
的轨迹为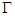 ,过点
,过点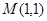 能否存在一条直线
能否存在一条直线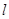 ,使
,使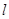 与曲线
与曲线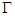 交于
交于 两点,且
两点,且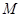 为线段
为线段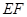 的中点,若存在求直线
的中点,若存在求直线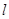 的方程,若不存在说明理由.(12分)
的方程,若不存在说明理由.(12分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com