
在60°的二面角M-a-N内有一点P,P到平面M、平面N的距离分别为1和2,求P点到直线a的距离.
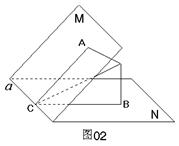
本题涉及点到平面的距离,点到直线的距离,二面角的平面角等概念,图中都没有表示,按怎样的顺序先后作出相应的图形是解决本题的关键.可以有不同的作法,下面仅以一个作法为例,说明这些概念的特点,分别作PA⊥M,M是垂足,PB⊥N,N是垂足,先作了两条垂线,找出P点到两个平面的距离,其余概念要通过推理得出:于是PA、PB确定平面α,设α∩M=AC,α∩N=BC,c∈a.由于PA⊥M,则PA⊥a,同理PB⊥a,因此a⊥平面α,得a⊥PC.这样,∠ACB是二面角的平面角,PC是P点到直线a的距离,下面只要在四边形ACBP内,利用平面几何的知识在△PAB中求出AB,再在△ABC中利用正弦定理求外接圆直径2R=![]() ,即为P点到直线a的距离,为
,即为P点到直线a的距离,为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:高中数学 来源:黄冈中学 高二数学(下册)、考试卷3 空间的角度与距离同步测试卷 题型:013
在60°的二面角α-a-β的面α内,AB⊥a于B,AB=2,在面β内,CD⊥a于D,CD=3,BD=1,M是a上的一个动点,则AM+CM的最小值为
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源:湖北省荆州中学2008高考复习立体几何基础题题库一(有详细答案)人教版 人教版 题型:044
在
60°的二面角M-a-N内有一点P,P到平面M、平面N的距离分别为1和2,求P点到直线a的距离.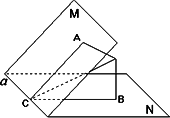
查看答案和解析>>
科目:高中数学 来源:广西南宁二中2011届高三5月月考数学理综试题 题型:022
已知球O的表面积为16π,且球心O在60°的二面角![]() 内部,若平面α与球相切于M点,平面β与球相截,且截面圆O1的半径为
内部,若平面α与球相切于M点,平面β与球相截,且截面圆O1的半径为![]() ,P为圆O1的圆周上任意一点,则M、P两点的球面距离的最值为__________.
,P为圆O1的圆周上任意一点,则M、P两点的球面距离的最值为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com