
【题目】设数列{an}的前n项和为Sn , 且Sn=2an﹣3n,(n∈N*).
(1)证明数列{an+3}为等比数列
(2)求{Sn}的前n项和Tn .
【答案】
(1)证明:令n=1,S1=2a1﹣3.∴a1=3
由 Sn+1=2an+1﹣3(n+1),Sn=2an﹣3n,
两式相减,得 an+1=2an+1﹣2an﹣3,
则 an+1=2an+3
an+1+3=2(an+3), ![]()
所以{an+3}为公比为2的等比数列
(2)解:an+3=(a1+3)2n﹣1=62n﹣1,
∴an=62n﹣1﹣3 …(10分)
![]() .
.
![]()
【解析】(1)利用当n≥2时,Sn﹣Sn﹣1=an , 可得得an=2an﹣1+3,从而可构造等比数列求解an+3,进而可以判定{an+1}是等比数列;(2)通过求出数列{an+3} 的通项公式得出数列{an}的通项公式,再求和即可.
【考点精析】掌握等比关系的确定和数列的前n项和是解答本题的根本,需要知道等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断;数列{an}的前n项和sn与通项an的关系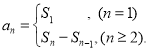 .
.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(1,sinx),
=(1,sinx), ![]() =(cos(2x+
=(cos(2x+ ![]() ),sinx),函数f(x)=
),sinx),函数f(x)= ![]()
![]() ﹣
﹣ ![]() cos2x
cos2x
(1)求函数f(x)的解析式及其单调递增区间;
(2)当x∈[0, ![]() ]时,求函数f(x)的值域.
]时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】20名同学参加某次数学考试成绩(单位:分)的频率分布直方图如下:
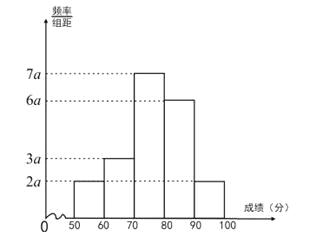
(Ⅰ)求频率分布直方图中![]() 的值;
的值;
(Ⅱ)分别求出成绩落在![]() ,
, ![]() 中的学生人数;
中的学生人数;
(Ⅲ)从成绩在![]() 的学生中任选2人,求此2人的成绩都在
的学生中任选2人,求此2人的成绩都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(1)求![]() 到平面
到平面![]() 的距离
的距离
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】福利彩票“双色球”中红球的号码可以从01,02,03,…,32,33这33个二位号码中选取,小明利用如图所示的随机数表选取红色球的6个号码,选取方法是从第1行第9列和第10列的数字开始从左到右依次选取两个数字,则第四个被选中的红色球号码为( )
81 47 23 68 63 93 17 90 12 69 86 81 62 93 50 60 91 33 75 85 61 39 85 |
06 32 35 92 46 22 54 10 02 78 49 82 18 86 70 48 05 46 88 15 19 20 49 |
A. 12 B. 33 C. 06 D. 16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .数列
.数列![]() 的前n项和为
的前n项和为![]() ,满足
,满足![]() ,
, ![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)数列![]() 能否为等差数列?若能,求其通项公式;若不能,试说明理由;
能否为等差数列?若能,求其通项公式;若不能,试说明理由;
(3)若数列![]() 是各项均为正整数的递增数列,设
是各项均为正整数的递增数列,设![]() ,则当
,则当![]() ,
, ![]() ,
, ![]() 和
和![]() ,
, ![]() ,
, ![]() 均成等差数列时,求正整数
均成等差数列时,求正整数![]() ,
, ![]() ,
, ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆F1:(x+1)2+y2=16,定点F2(1,0),A是圆F1上的一动点,线段F2A的垂直平分线交半径F1A于P点.
(1)求P点的轨迹C的方程;
(2)四边形EFGH的四个顶点都在曲线C上,且对角线EG,FH过原点O,
若kEGkFH=-![]() ,求证:四边形EFGH的面积为定值,并求出此定值.
,求证:四边形EFGH的面积为定值,并求出此定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com