Question

【题目】定义在R上的函数f（x）满足f（x）+f（x+5）=16，当x∈（﹣1，9）时，f（x）=x2﹣2x ， 则函数f（x）在[0，2016]上的零点个数是 ．

Answer 1

【答案】605
【解析】解：∵f（x）+f（x+5）=16，
f（x+5）+f（x+10）=16，
两式相减得，f（x）=f（x+10），
故f（x）为周期为10的函数，x∈（﹣1，9）时，
令f（x）=x2﹣2x=0得：x2=2x ，
在同一坐标系中作出y=x2与y=2x的图象如下，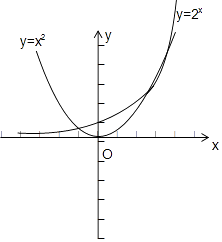

由图知，当x∈（﹣1，4]时，函数f（x）=x2﹣2x有3个零点（y轴右侧的两个零点为2和4），
∵f’（x）=2x﹣2xln2，∴当x∈（4，9）时，f’（x）＜0，函数单调减，即无零点，
综上：函数f（x）在一个周期内有三个零点，
=201+6，
就是说在区间在[0，2016]上有201个完整周期，这201个周期内共603个零点，在[0，6]内有二个零点，
∴函数f（x）在[0，2016]上共有605个零点，
所以答案是：605．