
【题目】对于定义在区间D上的函数![]() ,若存在闭区间
,若存在闭区间![]() 和常数
和常数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,且对任意
,且对任意![]() ∈D,当
∈D,当![]() 时,
时,![]() 恒成立,则称函数
恒成立,则称函数![]() 为区间D上的“平底型”函数.
为区间D上的“平底型”函数.
(Ⅰ)判断函数![]() 和
和![]() 是否为R上的“平底型”函数? 并说明理由;
是否为R上的“平底型”函数? 并说明理由;
(Ⅱ)设![]() 是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式
是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式![]() 对一切
对一切![]() R恒成立,求实数
R恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若函数![]() 是区间
是区间![]() 上的“平底型”函数,求
上的“平底型”函数,求![]() 和
和![]() 的值.
的值.
.
【答案】(1)![]() 不是“平底型”函数(2)实数
不是“平底型”函数(2)实数![]() 的范围是
的范围是![]() ⑶m=1,n=1
⑶m=1,n=1
【解析】
【解】(1)对于函数![]() ,当
,当![]() 时,
时,![]() .
.
当![]() 或
或![]() 时,
时,![]() 恒成立,故
恒成立,故![]() 是“平底型”函数
是“平底型”函数
……………………………………………………………2分
对于函数![]() ,当
,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
所以不存在闭区间![]() ,使当
,使当![]() 时,
时,![]() 恒成立.
恒成立.
故![]() 不是“平底型”函数. ……………………………………4分
不是“平底型”函数. ……………………………………4分
![]() (Ⅱ)若
(Ⅱ)若![]() 对一切
对一切![]() R恒成立,则
R恒成立,则![]() .
.
因为![]() ,所以
,所以![]() .又
.又![]() ,则
,则![]() . ……6分
. ……6分
因为![]() ,则
,则![]() ,解得
,解得![]() .
.
故实数![]() 的范围是
的范围是![]() . …………………………………………………8分
. …………………………………………………8分
(Ⅲ)因为函数![]() 是区间
是区间![]() 上的“平底型”函数,则
上的“平底型”函数,则
存在区间![]()
![]() 和常数
和常数![]() ,使得
,使得![]() 恒成立.
恒成立.
所以![]() 恒成立,即
恒成立,即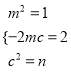 .解得
.解得![]() 或
或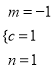 . ……10分
. ……10分
当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() 恒成立.
恒成立.
此时,![]() 是区间
是区间![]() 上的“平底型”函数. ………………12分
上的“平底型”函数. ………………12分
当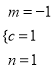 时,
时,![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
此时,![]() 不是区间
不是区间![]() 上的“平底型”函数. ………………13分
上的“平底型”函数. ………………13分
综上分析,m=1,n=1为所求. ………………………………………14分


科目:高中数学 来源: 题型:
【题目】某池塘中原有一块浮草,浮草蔓延后的面积![]() (平方米)与时间
(平方米)与时间![]() (月)之间的函数关系式是
(月)之间的函数关系式是![]() 且
且![]() ,它的图象如图所示,给出以下命题:①池塘中原有浮草的面积是
,它的图象如图所示,给出以下命题:①池塘中原有浮草的面积是![]() 平方米;②第
平方米;②第![]() 个月浮草的面积超过
个月浮草的面积超过![]() 平方米;③浮草每月增加的面积都相等;④若浮草面积达到
平方米;③浮草每月增加的面积都相等;④若浮草面积达到![]() 平方米,
平方米,![]() 平方米,
平方米,![]() 平方米所经过的时间分别为
平方米所经过的时间分别为![]() ,则
,则![]() .其中正确命题的序号有_____.(注:请写出所有正确结论的序号)
.其中正确命题的序号有_____.(注:请写出所有正确结论的序号)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣4x﹣6y+12=0,点A(3,5).
(1)将圆C的方程化为标准方程,并写出圆C的圆心坐标及半径r;
(2)求过点A的圆的切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到焦点
到焦点![]() 的距离
的距离![]() ,倾斜角为
,倾斜角为![]() 的直线经过焦点
的直线经过焦点![]() ,且与抛物线交于两点
,且与抛物线交于两点![]() 、
、![]() .
.
(1)求抛物线的标准方程及准线方程;
(2)若![]() 为锐角,作线段
为锐角,作线段![]() 的中垂线
的中垂线![]() 交
交![]() 轴于点
轴于点![]() .证明:
.证明:![]() 为定值,并求出该定值.
为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2018·湖南师大附中摸底)已知直线l经过点P(-4,-3),且被圆(x+1)2+(y+2)2=25截得的弦长为8,则直线l的方程是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年9月24日,阿贝尔奖和菲尔兹奖双料得主、英国著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想,这一事件引起了数学届的震动。在1859年的时候,德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题,也就是著名的黎曼猜想。在此之前,著名数学家欧拉也曾研究过这个问题,并得到小于数字![]() 的素数个数大约可以表示为
的素数个数大约可以表示为![]() 的结论。若根据欧拉得出的结论,估计1000以内的素数的个数为_________(素数即质数,
的结论。若根据欧拉得出的结论,估计1000以内的素数的个数为_________(素数即质数,![]() ,计算结果取整数)
,计算结果取整数)
A. 768 B. 144 C. 767 D. 145
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】按照我国《机动车交通事故责任强制保险条例》规定,交强险是车主必须为机动车购买的险种,若普通7座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是保费浮动机制,保费与上一、二、三个年度车辆发生道路交通事故的情况相关联,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
元,在下一年续保时,实行的是保费浮动机制,保费与上一、二、三个年度车辆发生道路交通事故的情况相关联,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
交强险浮动因素和浮动费率比率表 | ||
投保类型 | 浮动因素 | 浮动比率 |
| 上一个年度未发生有责任道路交通事故 | 下浮10% |
| 上两个年度未发生有责任道路交通事故 | 下浮20% |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| 上一个年度发生两次及两次以上有责任不涉及死亡的道路交通事故 | 上浮10% |
| 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机构为了研究某一品牌普通7座以下私家车的投保情况,随机抽取了80辆车龄已满三年的该品牌同型号私家车在下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
| |
数量 | 20 | 10 | 10 | 20 | 15 | 5 |
以这80辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)某家庭有一辆该品牌车且车龄刚满三年,记![]() 为该车在第四年续保时的费用,求
为该车在第四年续保时的费用,求![]() 的分布列;
的分布列;
(2)某销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基准保费的车辆记为事故车.
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至少有2辆事故车的概率;
②假设购进一辆事故车亏损4000元,一辆非事故盈利8000元,若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求其获得利润的期望值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com