练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数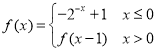,则下列命题中正确命题的个数是（ ）

    ①函数在上为周期函数

    ②函数在区间,上单调递增

    ③函数在（）取到最大值,且无最小值

    ④若方程（）有且仅有两个不同的实根,则

    A.个B.个C.个D.个

    【答案】B

    【解析】

    作出的图像,由图像对各选项进行判断即可.时,,可由的图像作关于轴的对称图像,再向上平移一个单位得到.当时,故是周期为的周期函数,图像可由时,向右平移一个单位得到,根据周期函数的性质即可得到图像.

    的图像如图所示:

    对于①,因为,,可得所以函数在上不是周期函数,故①不正确;

    对于②,当,结合函数图像可知,函数在区间,上单调递增,故②正确;

    对于③,因为时,,不是最大值, 故③不正确;

    对于④,如图所示,

    图中两条曲线对应的分别为和,故方程为,有且只有两个实根,则 ,故④正确.

    故选:B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在我们的教材必修一中有这样一个问题，假设你有一笔资金，现有三种投资方案供你选择，这三种方案的回报如下:

    方案一：每天回报元；

    方案二：第一天回报元，以后每天比前一天多回报元；

    方案三：第一天回报元，以后每天的回报比前一天翻一番.

    记三种方案第天的回报分别为，，.

    （1）根据数列的定义判断数列，，的类型，并据此写出三个数列的通项公式；

    （2）小王准备做一个为期十天的短期投资，他应该选择哪一种投资方案？并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，

    （1）求当在处的切线的斜率最小时，的解析式；

    （2）在（1）的条件下，是否总存在实数m，使得对任意的，总存在，使得成立？若存在，求出实数m的取值范围；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    已知在极坐标系中，点，，是线段的中点，以极点为原点，极轴为轴的正半轴，并在两坐标系中取相同的长度单位，建立平面直角坐标系，曲线的参数方程是（为参数）.

    （1）求点的直角坐标，并求曲线的普通方程；

    （2）设直线过点交曲线于两点，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）当时，求不等式的解集；

    （2）若，且对任意，恒成立，求的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中．

    （Ⅰ）当时，求曲线在点处的切线方程；

    （Ⅱ）若函数有唯一零点，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中，、分别为、的中点，，，.

    ⑴求证：平面；

    ⑵求二面角的正弦值；

    ⑶已知为棱上的点，若，求线段的长度.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝lnx，a∈R．

    （1）若x＝2是函数f（x）的极值点，求曲线y＝f（x）在点（1，f（1））处的切线方程；

    （2）若x＞1时，f（x）＞0，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知△ABC的内角A，B，C的对边分别为a，b，c．

    （1）若的面积，求a+c值；

    （2）若2cosC（+）=c2，求角C．

    查看答案和解析>>

    同步练习册答案