
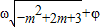 )>Asin(
)>Asin(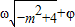 )?若存在,求出m值(或范围),若不存在,请说明理由.
)?若存在,求出m值(或范围),若不存在,请说明理由.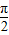 ≤
≤ x+
x+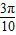 ≤2kπ+
≤2kπ+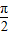 ,解此不等式,即可求得函数的单调递增区间;
,解此不等式,即可求得函数的单调递增区间;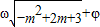 和
和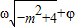 的范围,确定函数在该区间上的单调性,即可求得结果.
的范围,确定函数在该区间上的单调性,即可求得结果. [3-(-3)]=3,
[3-(-3)]=3,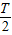 =5π,
=5π,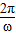 ,
,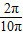 =
= ,
, π+ϕ=
π+ϕ=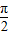 ,
,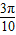 ,
, x+
x+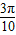 ),
),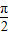 ≤
≤ x+
x+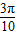 ≤2kπ+
≤2kπ+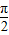 得10kπ-4π≤x≤10kπ+π,k∈Z
得10kπ-4π≤x≤10kπ+π,k∈Z ,ϕ=
,ϕ=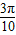 ,
,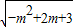 +ϕ=
+ϕ=
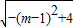 +
+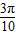 ∈(0,
∈(0, ),
),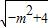 +ϕ=
+ϕ=
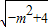 +
+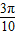 ∈(0,
∈(0,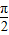 ),
), )上是增函数
)上是增函数
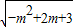 +
+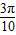 >
>
 +
+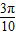 ,
,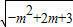 >
>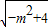
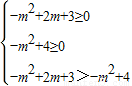 ,
,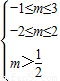 解得:
解得: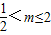 .
.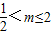 .
.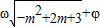 ∈(0,
∈(0, ),
),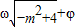 ∈(0,
∈(0,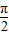 )的分析与应用,考查灵活应用知识分析解决问题的能力和运算能力,体现了转化的数学思想方法,属于难题.
)的分析与应用,考查灵活应用知识分析解决问题的能力和运算能力,体现了转化的数学思想方法,属于难题. 

科目:高中数学 来源: 题型:
| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,是函数y=Asin(ωx+φ),(-π<φ<π)的图象的一段,O是坐标原点,P是图象的最高点,A点坐标为(5,0),若|
如图,是函数y=Asin(ωx+φ),(-π<φ<π)的图象的一段,O是坐标原点,P是图象的最高点,A点坐标为(5,0),若|| OP |
| 10 |
| OP |
| OA |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com