已知抛物线W:y=ax2经过点A(2,1),过A作倾斜角互补的两条不同的直线L1,L2.
(1)求抛物线W的方程及其准线方程;
(2)当直线L1与抛物线W相切时,求直线L2与抛物线W所围成封闭区域的面积;
(3)设直线L1、L2分别交抛物线W于B、C两点(均不与A重合),若以BC为直径的圆与抛物线的准线相切,求直线BC的方程.
【答案】
分析:(1)由于抛物线经过点(2,1),则点的坐标满足抛物线的解析式,即可求出a;
(2)由于直线L
1与抛物线相切,则可求L
1的斜率,亦可得L
2的斜率进而求出L
2的直线,由题意可知联立直线L
2与抛物线的方程,再利用定积分可求出围成封闭区域的面积;
(3)由于直线L
1、L
2分别交抛物线W于B、C两点(均不与A重合),则两直线的斜率都存在.故可设其中一条直线的斜率k,求出与抛物线的交点B,进而表示出另一条的斜率和交点C,又由圆以BC为直径,所以可用k表示出圆心和半径,由于以BC为直径的圆与抛物线的准线相切,所以圆心到准线的距离等于半径,得到关于k的等式,解出k,即可求出直线BC.
解答:解:(1)∵A(2,1)在y=ax
2上∴1=4a,即a=

∴所求W方程为y=

x
2,其准线方程为y=-1 …(2分)
(2)当直线L
1与抛物线W相切时,
由y′|
x=2=1可得L
1的斜率为1
∴L
2的斜率为-1,又L
2过A(2,1)
∴L
2方程为:y=-x+3,代入y=

x
2得:x
2+4x-12=0⇒x
1=2,x
2=-6 …(4分)
∴S=

…(6分)
(3)不妨设AB方程为y-1=k(x-2)(k>0)…(7分)
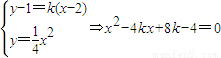
解得x=2或x=4k-2,∴B(4k-2,4k
2-4k+1)…(8分)
又AC斜率为-k,同理可得C(-4k-2,4k
2+4k+1)
∴|BC|=8

k …(10分)
线段BC中点为H(-2,4k
2+1),
∵以BC为直径的圆与准线y=-1相切,
∴(4k
2+1)-(-1)=4
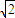
k∴k=
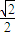
…(11分)
此时B(2
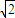
-2,3-2
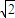
),C(-2
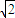
-2,3+2
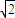
)
∴直线BC方程为:y-(3-2

)=-[x-(2
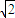
-2)]
即x+y-1=0 …(13分)
点评:本题考查直线与抛物线的位置关系,同时考查导数的几何意义.直线与圆锥曲线的位置关系是高考必考的内容,要切实掌握好.


 x2,其准线方程为y=-1 …(2分)
x2,其准线方程为y=-1 …(2分) x2
x2 …(6分)
…(6分)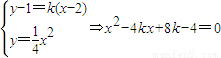
 k …(10分)
k …(10分)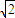 k∴k=
k∴k=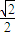 …(11分)
…(11分)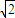 -2,3-2
-2,3-2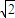 ),C(-2
),C(-2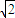 -2,3+2
-2,3+2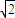 )
) )=-[x-(2
)=-[x-(2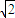 -2)]
-2)]
