
(1)求三棱锥C—ADE的体积;
(2)求直线BA和平面ADE所成的角的大小;
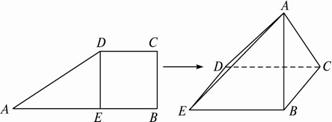
(1)解:在立体图形中,由题意得AB⊥平面BCDE,又知BD⊥CD,根据三垂线定理得AC⊥CD.故∠ACB就是二面角ACDB的平面角,于是∠ACB=45°,?
从而得AB=1,AC=![]() ,AE=
,AE=![]() ,?
,?
又因为BC∥DE,∴BC∥平面ADE.?
VC—ADE=VB—ADE=VA—BDE=![]() SBDE·AB=
SBDE·AB=![]() ×(
×(![]() SBCDE)·AB=
SBCDE)·AB=![]() ×(
×(![]() ×1×1)×1=
×1×1)×1=![]() . ?
. ?
(2)解:∵AB⊥平面BCDE,∴AB⊥DE,而DE⊥BE,?
∴DE⊥平面ABE,∴平面ADE⊥平面ABE,在△ABE中过点B作BF⊥AE于F,则BF⊥平面ADE.于是∠BAF就是所求的直线AB和平面ADE所成的角.在RT△ABE中,AB=BE=1.?
∴∠BAF=45°.?
∴直线AB和平面ADE所成的角的大小为45°.


科目:高中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
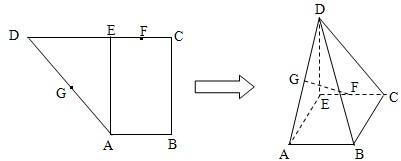
 如图,直角梯形ABCD中,BC∥AD,BA⊥AD,PA⊥面ABCD,E是PD的中点,过BC和点E的平面与PA交于点F,且PA=AB=BC=2,AD=4.
如图,直角梯形ABCD中,BC∥AD,BA⊥AD,PA⊥面ABCD,E是PD的中点,过BC和点E的平面与PA交于点F,且PA=AB=BC=2,AD=4.查看答案和解析>>
科目:高中数学 来源: 题型:
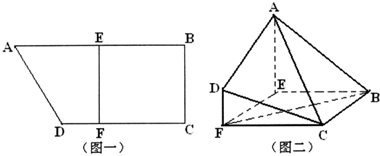 (2011•徐州模拟)在直角梯形ABCD中,AB∥CD,AB=2BC=4,CD=3,E为AB中点,过E作EF⊥CD,垂足为F,(如图一),将此梯形沿EF折起,使得平面ADFE垂直于平面FCBE,(如图二).
(2011•徐州模拟)在直角梯形ABCD中,AB∥CD,AB=2BC=4,CD=3,E为AB中点,过E作EF⊥CD,垂足为F,(如图一),将此梯形沿EF折起,使得平面ADFE垂直于平面FCBE,(如图二).查看答案和解析>>
科目:高中数学 来源: 题型:
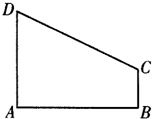 如图,直角梯形ABCD中,∠DAB=90°,AD∥BC,AB=2,AD=
如图,直角梯形ABCD中,∠DAB=90°,AD∥BC,AB=2,AD=| 3 |
| 2 |
| 1 |
| 2 |
| EC |
| 1 |
| 2 |
| AB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com