
【题目】已知函数 ![]() 是奇函数,f(x)=lg(10x+1)+bx是偶函数.
是奇函数,f(x)=lg(10x+1)+bx是偶函数.
(1)求a+b的值.
(2)若对任意的t∈[0,+∞),不等式g(t2﹣2t)+g(2t2﹣k)>0恒成立,求实数k的取值范围.
(3)设 ![]() ,若存在x∈(﹣∞,1],使不等式g(x)>h[lg(10a+9)]成立,求实数a的取值范围.
,若存在x∈(﹣∞,1],使不等式g(x)>h[lg(10a+9)]成立,求实数a的取值范围.
【答案】
(1)解:由g(0)=0得a=1,则 ![]() ,经检验g(x)是奇函数.
,经检验g(x)是奇函数.
由f(﹣1)=f(1)得 ![]() ,则
,则 ![]() ,经检验f(x)是偶函数,
,经检验f(x)是偶函数,
∴ ![]() .
.
(2)解:∵ ![]() ,且g(x)在(﹣∞,+∞)单调递增,且g(x)为奇函数.
,且g(x)在(﹣∞,+∞)单调递增,且g(x)为奇函数.
∴由g(t2﹣2t)+g(2t2﹣k)>0恒成立,得g(t2﹣2t)>﹣g(2t2﹣k)=g(﹣2t2+k),
∴t2﹣2t>﹣2t2+k,t∈[0,+∞)恒成立,
即3t2﹣2t>k,t∈[0,+∞)恒成立,
令F(x)=3t2﹣2t,在[0,+∞)上F(x)的最小值为 ![]() ,∴
,∴ ![]() .
.
(3)解:h(x)=lg(10x+1),h(lg(10a+9))=lg[10lg(10a+9)+1]=lg(10a+10),
则由已知得,存在x∈(﹣∞,1],使不等式g(x)>lg(10a+10)成立,
而g(x)在(﹣∞,1]单增,∴ ![]() ,
,
∴ ![]() ,∴
,∴ ![]() .
.
又 ![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() .
.
【解析】(1)由条件利用函数的奇偶性的性质求得a、b的值,可得a+b的值.(2)由条件利用函数的单调性求得3t2﹣2t>k,t∈[0,+∞)恒成立,求得3t2﹣2t的最小值,可得k的范围.(3)由题意可得存在x∈(﹣∞,1],使不等式g(x)>lg(10a+10)成立,求得g(x)的最大值,可得a的范围.
【考点精析】解答此题的关键在于理解函数单调性的判断方法的相关知识,掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较,以及对函数奇偶性的性质的理解,了解在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为角A,B,C所对的边,角C是钝角,且sinB= ![]() .
.
(1)求角C的值;
(2)若b=2,△ABC的面积为 ![]() ,求c的值.
,求c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.命题“若x≠2或y≠7,则x+y≠9”的逆命题为真命题
B.命题“若x2=4,则x=2”的否命题是“若x2=4,则x≠2”
C.命题“若x2<1,则﹣1<x<1”的逆否命题是“若x<﹣1或x>1,则x2>1”
D.若命题p:x∈R,x2﹣x+1>0,q:x0∈(0,+∞),sinx0>1,则(¬p)∨q为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系内,已知A(3,3)是⊙C上一点,折叠该圆两次使点A分别与圆上不相同的两点(异于点A)重合,两次的折痕方程分别为x﹣y+1=0和x+y﹣7=0,若⊙C上存在点P,使∠MPN=90°,其中M、N的坐标分别为(﹣m,0)(m,0),则m的最大值为( )
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产甲、乙两种产品所得利润分别为P和Q(万元),它们与投入资金m(万元)的关系有经验公式P= ![]() m+65,Q=76+4
m+65,Q=76+4 ![]() ,今将150万元资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投资金额不低于25万元.
,今将150万元资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投资金额不低于25万元.
(1)设对乙产品投入资金x万元,求总利润y(万元)关于x的函数关系式及其定义域;
(2)如何分配使用资金,才能使所得总利润最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(﹣2,2).
=(﹣2,2).
(1)若 ![]() =
= ![]() ,求(sinα+cosα)2的值;
,求(sinα+cosα)2的值;
(2)若 ![]() ,求sin(π﹣α)sin(
,求sin(π﹣α)sin( ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx﹣ ![]() )(其中A,ω为常数,且A>0,ω>0)的部分图象如图所示.
)(其中A,ω为常数,且A>0,ω>0)的部分图象如图所示. 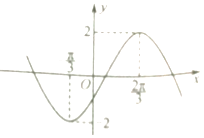
(1)求函数f(x)的解析式;
(2)若f(α+ ![]() )=
)= ![]() ,f(β+
,f(β+ ![]() )=
)= ![]() ,且α,β∈(0,
,且α,β∈(0, ![]() ),求α+β的值.
),求α+β的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com