
已知实数 ,函数
,函数 .
.
(1)当 时,求
时,求 的最小值;
的最小值;
(2)当 时,判断
时,判断 的单调性,并说明理由;
的单调性,并说明理由;
(3)求实数 的范围,使得对于区间
的范围,使得对于区间 上的任意三个实数
上的任意三个实数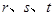 ,都存在以
,都存在以 为边长的三角形.
为边长的三角形.
(1)2;(2)递增;(3)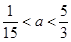 .
.
解析试题分析:(1)研究函数问题,一般先研究函数的性质,如奇偶性,单调性,周期性等等,如本题中函数 是偶函数,因此其最小值我们只要在
是偶函数,因此其最小值我们只要在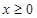 时求得即可;(2)
时求得即可;(2) 时,
时, 可化简为
可化简为 ,下面我们只要按照单调性的定义就可证明在
,下面我们只要按照单调性的定义就可证明在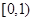 上函数是单调递增的,当然在
上函数是单调递增的,当然在 上是递减的;(3)处理此问题,首先通过换元法把问题简化,设
上是递减的;(3)处理此问题,首先通过换元法把问题简化,设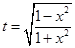 ,则函数
,则函数 变为
变为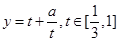 ,问题变为求实数
,问题变为求实数 的范围,使得在区间
的范围,使得在区间 上,恒有
上,恒有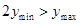 .对于函数
.对于函数 ,我们知道,它在
,我们知道,它在 上递减,在
上递减,在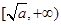 上递增,故我们要讨论它在区间
上递增,故我们要讨论它在区间 上的最大(小)值,就必须分类讨论,分类标准显然是
上的最大(小)值,就必须分类讨论,分类标准显然是 ,
,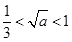 ,
,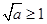 ,在
,在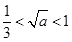 时还要讨论最大值在区间
时还要讨论最大值在区间 的哪个端点取得,也即共分成四类.
的哪个端点取得,也即共分成四类.
试题解析:易知 的定义域为
的定义域为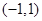 ,且
,且 为偶函数.
为偶函数.
(1) 时,
时, 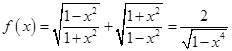 2分
2分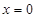 时
时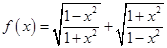 最小值为2. 4分
最小值为2. 4分
(2) 时,
时, 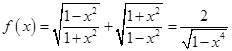
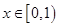 时,
时, 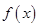 递增;
递增; 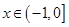 时,
时,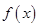 递减; 6分
递减; 6分 为偶函数.所以只对
为偶函数.所以只对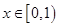 时,说明
时,说明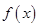 递增.
递增.
设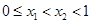 ,所以
,所以 ,得
,得
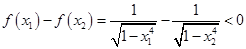
所以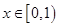 时,
时, 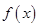 递增; 10分
递增; 10分
(3)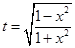 ,
,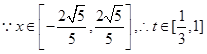 ,
,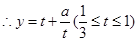
从而原问题等价于求实数 的范围,使得在区间
的范围,使得在区间 上,
上,
恒有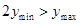 . 11分
. 11分
①当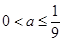 时,
时, 在
在 上单调递增,
上单调递增,  由
由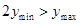 得
得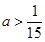 ,
,
从而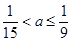 ; 12分
; 12分
②当 时,
时, 在
在 上单调递减,在
上单调递减,在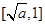 上单调递增,
上单调递增,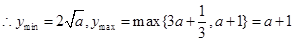 ,
,
由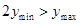 得
得 ,从而
,从而 ; 13分
; 13分
③当

 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:解答题
近日,国家经贸委发出了关于深入开展增产节约运动,大力增产市场适销对路产品的通知,并发布了当前国内市场185种适销工业品和42种滞销产品的参考目录.为此,一公司举行某产品的促销活动,经测算该产品的销售量P万件(生产量与销售量相等)与促销费用x万元满足 (其中
(其中 ,a为正常数).已知生产该产品还需投入成本10+2P万元(不含促销费用),产品的销售价格定为
,a为正常数).已知生产该产品还需投入成本10+2P万元(不含促销费用),产品的销售价格定为 元/件.
元/件.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
我国是水资源较贫乏的国家之一,各地采用价格调控等手段来达到节约用水的目的,某市每户每月用水收费办法是:水费=基本费+超额费+定额损耗费.且有如下两条规定:
①若每月用水量不超过最低限量 立方米,只付基本费10元加上定额损耗费2元;
立方米,只付基本费10元加上定额损耗费2元;
②若用水量超过 立方米时,除了付以上同样的基本费和定额损耗费外,超过部分每立方米加付
立方米时,除了付以上同样的基本费和定额损耗费外,超过部分每立方米加付 元的超额费.
元的超额费.
解答以下问题:(1)写出每月水费 (元)与用水量
(元)与用水量 (立方米)的函数关系式;
(立方米)的函数关系式;
(2)若该市某家庭今年一季度每月的用水量和支付的费用如下表所示:
| 月份 | 用水量(立方米) | 水费(元) |
| 一 | 5 | 17 |
| 二 | 6 | 22 |
| 三 |  | 12 |
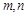 的值.
的值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=ax2+bx+1(a,b为实数),x∈R,F(x)=
(1)若f(-1)=0,且函数f(x) ≥0的对任意x属于一切实数成立,求F(x)的表达式;
(2)在 (1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数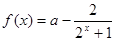 ,
,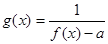 若函数
若函数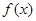 为奇函数,求
为奇函数,求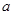 的值.
的值.
(2)若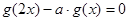 ,有唯一实数解,求
,有唯一实数解,求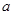 的取值范围.
的取值范围.
(3)若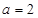 ,则是否存在实数
,则是否存在实数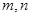
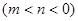 ,使得函数
,使得函数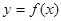 的定义域和值域都为
的定义域和值域都为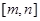 。若存在,求出
。若存在,求出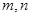 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com