
【题目】已知函数![]() ,在区间
,在区间![]() 上有最大值
上有最大值![]() ,最小值
,最小值![]() ,设函数
,设函数![]() .
.
(1)求![]() 的值;
的值;
(2)不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)方程![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用二次函数闭区间上的最值,通过a与0的大小讨论,列出方程,即可求a,b的值;
(2)转化不等式f(2x)﹣k2x≥0,为k在一侧,另一侧利用换元法通过二次函数在x∈[﹣1,1]上恒成立,求出最值,即可求实数k的取值范围;
(3)化简方程f(|2x﹣1|)+k(![]() 3)=0,转化为两个函数的图象的交点的个数,利用方程有三个不同的实数解,推出不等式然后求实数k的取值范围.
3)=0,转化为两个函数的图象的交点的个数,利用方程有三个不同的实数解,推出不等式然后求实数k的取值范围.
解:(1)g(x)=a(x﹣1)2+1+b﹣a,
∵a>0,∴g(x)在[2,3]上为增函数,
故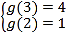 ,可得
,可得 ![]() ,
,![]() .
.
∴a=1,b=0
(2)方程f(2x)﹣k2x≥0化为2x![]() 2≥k2x,
2≥k2x,
k≤1![]()
令![]() t,k≤t2﹣2t+1,
t,k≤t2﹣2t+1,
∵x∈[﹣1,1],∴t![]() ,记φ(t)=t2﹣2t+1,
,记φ(t)=t2﹣2t+1,
∴φ(t)min=φ(1)=0,
∴k≤0.
(3)由f(|2x﹣1|)+k(![]() 3)=0
3)=0
得|2x﹣1|![]() (2+3k)=0,
(2+3k)=0,
|2x﹣1|2﹣(2+3k)|2x﹣1|+(1+2k)=0,|2x﹣1|≠0,
令|2x﹣1|=t,则方程化为t2﹣(2+3k)t+(1+2k)=0(t≠0),
∵方程|2x﹣1|![]() (2+3k)=0有三个不同的实数解,
(2+3k)=0有三个不同的实数解,
∴由t=|2x﹣1|的图象(如图)知,

t2﹣(2+3k)t+(1+2k)=0有两个根t1、t2,且0<t1<1<t2或0<t1<1,t2=1,
记φ(t)=t2﹣(2+3k)t+(1+2k),
则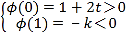 或
或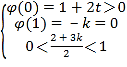
∴k>0.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点 ,顺次连接椭圆的四个顶点得到的四边形的面积为
,顺次连接椭圆的四个顶点得到的四边形的面积为![]() ,点
,点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)已知点![]() ,是椭圆
,是椭圆![]() 上的两点.
上的两点.
(ⅰ)若![]() ,且
,且![]() 为等边三角形,求
为等边三角形,求![]() 的面积;
的面积;
(ⅱ)若![]() ,证明:
,证明: ![]() 不可能为等边三角形.
不可能为等边三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() =2px经过点
=2px经过点![]() (1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(Ⅰ)求直线l的斜率的取值范围;
(Ⅱ)设O为原点,![]() ,
,![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题
①函数![]() 与函数
与函数![]() 表示同一个函数;
表示同一个函数;
②奇函数的图像一定通过直角坐标系的原点;
③若函数![]() 的定义域为
的定义域为![]() ,则函数
,则函数![]() 的定义域为
的定义域为![]() ;
;
④设函数![]() 是在区间
是在区间![]() 上图像连续的函数,且
上图像连续的函数,且![]() ,则方程
,则方程![]() 在区间
在区间![]() 上至少有一实根;
上至少有一实根;
其中正确命题的序号是( )
A.(1)B.(2)C.(3)D.(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国自改革开放以来,生活越来越好,肥胖问题也目渐显著,为分析肥胖程度对总胆固醇与空腹血糖的影响,在肥胖人群中随机抽出8人,他们的肥胖指数![]() 值、总胆固醇
值、总胆固醇![]() 指标值单位:
指标值单位: ![]() )、空腹血糖
)、空腹血糖![]() 指标值(单位:
指标值(单位: ![]() )如下表所示:
)如下表所示:

(1)用变量![]() 与
与![]() 与
与![]() 的相关系数,分别说明
的相关系数,分别说明![]() 指标值与
指标值与![]() 值、
值、![]() 指标值与
指标值与![]() 值的相关程度;
值的相关程度;
(2)求![]() 与
与![]() 的线性回归方程,已知
的线性回归方程,已知![]() 指标值超过5.2为总胆固醇偏高,据此模型分析当
指标值超过5.2为总胆固醇偏高,据此模型分析当![]() 值达到多大时,需要注意监控总胆固醇偏高情况的出现(上述数据均要精确到0.01)
值达到多大时,需要注意监控总胆固醇偏高情况的出现(上述数据均要精确到0.01)
参考公式:相关系数
 ,
,  ,
,![]() .
.
参考数据: ![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用水清洗一堆蔬菜上残留的农药,对用一定量的水清洗一次的效果作如下假定:用1个单位量的水可洗掉蔬菜上残留农药量的![]() ,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用
,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用![]() 单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数
单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数![]() .
.
(1)试规定![]() 的值,并解释其实际意义;
的值,并解释其实际意义;
(2)试根据假定写出函数![]() 应该满足的条件和具有的性质;
应该满足的条件和具有的性质;
(3)设![]() .现有
.现有![]() 单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次,试问用哪种方案清洗后蔬菜上残留的农药量比较省?说明理由.
单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次,试问用哪种方案清洗后蔬菜上残留的农药量比较省?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为 ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 与曲线
与曲线![]() 两交点所在直线的极坐标方程;
两交点所在直线的极坐标方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与曲线
,与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(x﹣1)(a>0,且a≠1).
(1)若f(x)在[2,9]上的最大值与最小值之差为3,求a的值;
(2)若a>1,求不等式f(2x)>0的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com