
【题目】已知椭圆![]() ,对于任意实数
,对于任意实数![]() ,椭圆被下列直线所截得的弦长与被直线
,椭圆被下列直线所截得的弦长与被直线![]() 所截得的弦长不可能相等的是( )
所截得的弦长不可能相等的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】D
【解析】分析:当![]() 过点
过点![]() 时,直线
时,直线![]() 和选项A中的直线重合,故不能选 A.
和选项A中的直线重合,故不能选 A.
当l![]() 过点(1,0)时,直线
过点(1,0)时,直线![]() 和选项D中的直线关于y轴对称,被椭圆E所截得的弦长相同,
和选项D中的直线关于y轴对称,被椭圆E所截得的弦长相同,
当k=0时,直线l和选项B中的直线关于x轴对称,被椭圆E所截得的弦长相同.排除A、B、D.
详解:由数形结合可知,当![]() 过点
过点![]() 时,直线
时,直线![]() 和选项A中的直线重合,故不能选 A.
和选项A中的直线重合,故不能选 A.
当![]() 过点(1,0)时,直线
过点(1,0)时,直线![]() 和选项C中的直线关于
和选项C中的直线关于![]() 轴对称,被椭圆E所截得的弦长相同,故不能选C.
轴对称,被椭圆E所截得的弦长相同,故不能选C.
当![]() 时,直线
时,直线![]() 和选项B中的直线关于
和选项B中的直线关于![]() 轴对称,被椭圆E所截得的弦长相同,故不能选B.
轴对称,被椭圆E所截得的弦长相同,故不能选B.
直线l![]() 斜率为
斜率为![]() ,在y轴上的截距为1;选项D中的直线
,在y轴上的截距为1;选项D中的直线![]() 斜率为
斜率为![]() ,在
,在![]() 轴上的截距为2,这两直线不关于
轴上的截距为2,这两直线不关于![]() 轴、
轴、![]() 轴、原点对称,故被椭圆E所截得的弦长不可能相等.
轴、原点对称,故被椭圆E所截得的弦长不可能相等.
故选:C.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+mx(m为常数).
(1)讨论函数f(x)的单调区间;
(2)当 ![]() 时,设
时,设 ![]() 的两个极值点x1 , x2(x1<x2)恰为h(x)=2lnx﹣ax﹣x2的零点,求
的两个极值点x1 , x2(x1<x2)恰为h(x)=2lnx﹣ax﹣x2的零点,求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点![]() 为圆心的圆
为圆心的圆![]() 被直线
被直线![]() :
:![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)求过![]() 与圆
与圆![]() 相切的直线方程;
相切的直线方程;
(3)若![]() 是
是![]() 轴的动点,
轴的动点,![]() ,
,![]() 分别切圆
分别切圆![]() 于
于![]() ,
,![]() 两点.试问:直线
两点.试问:直线![]() 是否恒过定点?若是,求出恒过点坐标;若不是,说明理由.
是否恒过定点?若是,求出恒过点坐标;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表:
组别 | PM2.5浓度 | 频数(天) | 频率 |
第一组 | (0,25] | 3 | 0.15 |
第二组 | (25,50] | 12 | 0.6 |
第三组 | (50,75] | 3 | 0.15 |
第四组 | (75,100] | 2 | 0.1 |
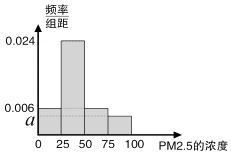
(1)将这20天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图. ①求图4中a的值;
②求样本平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
(2)将频率视为概率,对于2016年的某3天,记这3天中该居民区PM2.5的24小时平均浓度符合环境空气质量标准的天数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣a|+a.
(1)若不等式f(x)≤6的解集为{x|﹣2≤x≤3},求实数a的值;
(2)在(1)的条件下,若存在实数n使f(n)≤m﹣f(﹣n)成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,球![]() 的表面积为
的表面积为![]() ,球心
,球心![]() 为空间直角坐标系
为空间直角坐标系![]() 的原点,且球
的原点,且球![]() 分别与
分别与![]() 轴的正交半轴交于
轴的正交半轴交于![]() 三点,已知球面上一点
三点,已知球面上一点![]() .
.
(1)求![]() 两点在球
两点在球![]() 上的球面距离;
上的球面距离;
(2)过点![]() 作平面
作平面![]() 的垂线,垂足
的垂线,垂足![]() ,求
,求![]() 的坐标,并计算四面体
的坐标,并计算四面体![]() 的体积;
的体积;
(3)求平面![]() 与平面
与平面![]() 所成锐二面角的大小.
所成锐二面角的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次高中学科竞赛中,4000名考生的参赛成绩统计如图所示,60分以下视为不及格,若同一组中数据用该组区间中点作代表,则下列说法中有误的是( )

A. 成绩在![]() 分的考生人数最多
分的考生人数最多
B. 不及格的考生人数为1000人
C. 考生竞赛成绩的平均分约70.5分
D. 考生竞赛成绩的中位数为75分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期末考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是![]() .
.

(1)若成绩在![]() 的学生中男生比女生多一人,从成绩在
的学生中男生比女生多一人,从成绩在![]() 的学生中任选2人,求此2人都是男生的概率;
的学生中任选2人,求此2人都是男生的概率;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】兰天购物广场某营销部门随机抽查了100名市民在2018年国庆长假期间购物广场的消费金额,所得数据如表,已知消费金额不超过3千元与超过3千元的人数比恰为![]() .
.
消费金额(单位:千元) | 人数 | 频率 |
| 8 | 0.08 |
| 12 | 0.12 |
|
|
|
|
|
|
| 8 | 0.08 |
| 7 | 0.07 |
合计 | 100 | 1.00 |

(1)试确定![]() ,
,![]() ,
,![]() ,
,![]() 的值,并补全频率分布直方图(如图);
的值,并补全频率分布直方图(如图);
(2)用分层抽样的方法从消费金额在![]() 、
、![]() 和
和![]() 的三个群体中抽取7人进行问卷调查,则各小组应抽取几人?若从这7人中随机选取2人,则此2人来自同一群体的概率是多少?
的三个群体中抽取7人进行问卷调查,则各小组应抽取几人?若从这7人中随机选取2人,则此2人来自同一群体的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com