Question

已知圆C₁:x²+y²+2x+8y-8=0，圆C₂:x²+y²-4x-4y-2=0，判断两圆的位置关系.

Answer 1

解法一：圆C₁与圆C₂的方程联立得到方程组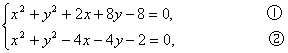

①-②得x+2y-1=0③,由③得y=，把上式代入①并整理得x²-2x-3=0④.

方程④的判别式Δ=(-2)²-4×1×(-3)=16＞0,所以方程④有两个不相等的实数根，即圆C₁与圆C₂相交.

解法二：把圆C₁：x²+y²+2x+8y-8=0,圆C₂:x²+y²-4x-4y-2=0,化为标准方程，得(x+1)²+(y+4)²=25与（x-2）²+(y-2)²=10，圆C₁的圆心是点（-1，-4），半径长r₁=5;圆C₂的圆心是点（2，2），半径长r₂=.圆C₁圆C₂的连心线的长为=3,圆C₁、圆C₂的半径长之和为r₁+r₂=5+,半径长之差为r₁-r₂=5.而5＜3＜5+,即r₁-r₂＜3＜r₁+r₂,所以圆C₁与圆C₂相交.

点评：判断两圆的位置关系一般情况下，先化为标准方程，再利用几何法判断较为准确直观.