
【题目】定义两个函数的关系:函数![]() 的定义域分别为
的定义域分别为![]() ,若对任意的
,若对任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() ,我们就称函数
,我们就称函数![]() 为
为![]() 的“子函数”.已知函数
的“子函数”.已知函数![]() ,
,![]() ,
,![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若![]() 为
为![]() 的一个“子函数”,求
的一个“子函数”,求![]() 的最小值.
的最小值.
【答案】(1)单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ,(2)
,(2)![]() .
.
【解析】
(1)求导,令![]() ,可得
,可得![]() 的单调递增区间;令
的单调递增区间;令![]() ,可得
,可得![]() 的单调递减区间;
的单调递减区间;
(2)根据![]() 的单调性求出
的单调性求出![]() 的取值范围,进而得到
的取值范围,进而得到![]() ,即
,即![]() 有实数解,从而得到
有实数解,从而得到![]() ,令
,令![]() ,可得
,可得![]() ,令
,令![]() ,则
,则![]() ,
,![]() ,利用换元法和函数的单调性即可得出结果.
,利用换元法和函数的单调性即可得出结果.
(1)![]() ,函数
,函数![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ;
;
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以函数![]() 的单调递减区间为
的单调递减区间为![]() ,
,
综上,函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .
.
(2)由(1)知,当![]() 时,函数
时,函数![]() 取得极小值,即最小值,
取得极小值,即最小值,
所以![]() ,
,
当![]() 时,
时,![]() ,
,
且![]() 为连续函数,只需
为连续函数,只需![]() ,
,
即![]() 有实数解,
有实数解,
即![]() ,因为
,因为![]() ,
,
则![]() ,
,
令![]() ,
,
即![]() 在区间
在区间![]() 上有实数解,
上有实数解,
将![]() 看成直线
看成直线![]() 上的点,
上的点,
令![]() ,则
,则![]() ,
,![]() ,
,
令![]() ,则
,则![]() ,
,
所以![]() 的最小值为
的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】为了整顿食品的安全卫生,食品监督部门对某食品厂生产甲、乙两种食品进行了检测调研,检测某种有害微量元素的含量,随机在两种食品中各抽取了10个批次的食品,每个批次各随机地抽取了一件,下表是测量数据的茎叶图(单位:毫克).

规定:当食品中的有害微量元素的含量在![]() 时为一等品,在
时为一等品,在![]() 为二等品,20以上为劣质品.
为二等品,20以上为劣质品.
(1)用分层抽样的方法在两组数据中各抽取5个数据,再分别从这5个数据中各选取2个,求甲的一等品数与乙的一等品数相等的概率;
(2)每生产一件一等品盈利50元,二等品盈利20元,劣质品亏损20元,根据上表统计得到甲、乙两种食品为一等品、二等品、劣质品的频率,分别估计这两种食品为一等品、二等品、劣质品的概率,若分别从甲、乙食品中各抽取1件,设这两件食品给该厂带来的盈利为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国著名数学家华罗庚先生曾说:数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图象研究函数的性质,也常用函数的解析式来琢磨函数的图象特征.如函数![]() 的图象大致为( )
的图象大致为( )
A. B.
B.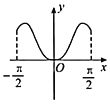
C.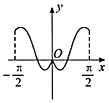 D.
D.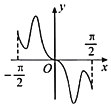
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-m|-|2x+2m|(m>0).
(Ⅰ)当m=1时,求不等式f(x)≥1的解集;
(Ⅱ)若x∈R,t∈R,使得f(x)+|t-1|<|t+1|,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 且
且![]() ).
).
(I)求直线![]() 的极坐标方程及曲线
的极坐标方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知![]() 是直线
是直线![]() 上的一点,
上的一点,![]() 是曲线
是曲线![]() 上的一点,
上的一点, ![]() ,
,![]() ,若
,若![]() 的最大值为2,求
的最大值为2,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() ,动圆
,动圆![]() 与圆
与圆![]() 外切并与圆
外切并与圆![]() 内切,圆心
内切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的方程;
的方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,问是否在
两点,问是否在![]() 轴上存在一点
轴上存在一点![]() ,使得当
,使得当![]() 变动时总有
变动时总有![]() ?若存在,请说明理由.
?若存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com