
【题目】已知函数![]() (其中
(其中![]() ),
),![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)若曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的单调区间和极值;
的单调区间和极值;
(2)若对任意![]() ,总存在
,总存在![]() 使得
使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)答案见解析;(2) ![]() .
.
【解析】试题分析:(1)![]() ,
, ![]() 算出m值,然后求出
算出m值,然后求出![]() 的单调区间和极值;
的单调区间和极值;
(2)因为对任意![]() ,总存在
,总存在![]() 使得
使得![]() ,
,
即![]() 成立,分别求
成立,分别求![]() 与
与![]() 的最值即可.
的最值即可.
试题解析:
(1)函数![]() 的定义域为
的定义域为![]() ,
, ![]() ,
,
在![]() 处的切线斜率为
处的切线斜率为![]() ,由
,由![]() ,∴
,∴![]() ,
,
∴![]() ,
, ![]() ,令
,令![]() ,得
,得![]() ,当
,当![]() 时,
时, ![]() ,
, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() ,
, ![]() 单调递增.从而
单调递增.从而![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ,当
,当![]() 时,
时, ![]() 有极小值
有极小值![]() ,
, ![]() 没有极大值;
没有极大值;
(2)由![]() ,
, ![]() ,当
,当![]() 时,
时, ![]() ,
, ![]() 单调递增,故
单调递增,故![]() 有最小值
有最小值![]() ,
,
因为对任意![]() ,总存在
,总存在![]() 使得
使得![]() ,
,
即![]() 成立,所以对任意
成立,所以对任意![]() ,都有
,都有![]() ,
,
即![]() ,
,
也即![]() 成立,从而对任意
成立,从而对任意![]() ,都有
,都有![]() 成立,
成立,
构造函数![]()
![]() ,则
,则![]() ,令
,令![]() ,得
,得![]() ,当
,当![]() 时,
时, ![]() ,
, ![]() 单调递增;当
单调递增;当![]() 时,
时, ![]() ,
, ![]() 单调递减,∴
单调递减,∴![]() 的最大值为
的最大值为![]() ,∴
,∴![]() ,综上,实数
,综上,实数![]() 的取值范围为
的取值范围为![]() .
.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且函数
,且函数![]() 是偶函数,设
是偶函数,设![]()
(1)求![]() 的解析式;
的解析式;
(2)若不等式![]() ≥0在区间(1,e2]上恒成立,求实数
≥0在区间(1,e2]上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若方程![]() 有三个不同的实数根,求实数
有三个不同的实数根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱![]() 中,三个侧面均为矩形,底面
中,三个侧面均为矩形,底面![]() 为等腰直角三角形,
为等腰直角三角形, ![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上运动.
上运动.
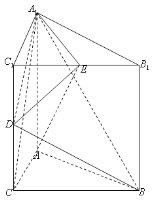
(1)求证![]()
![]()
![]() ;
;
(2)当点![]() 运动到某一位置时,恰好使二面角
运动到某一位置时,恰好使二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ,求点
,求点![]() 到平面
到平面![]() 的距离;
的距离;
(3)在(2)的条件下,试确定线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,确定其位置;若不存在,说明理由.
?若存在,确定其位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的两个焦点分别为F1(-1,0)、F2(1,0),短轴的两个端点分别为B1,B2
(1)若△F1B1B2为等边三角形,求椭圆C的方程;
(2)若椭圆C的短轴长为2,过点F2的直线l与椭圆C相交于P,Q两点,且![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续![]() 天,每天新增疑似病例不超过
天,每天新增疑似病例不超过![]() 人”.过去
人”.过去![]() 日,甲、乙、丙、丁四地新增疑似病例数据信息如下,则一定符合该标志的是( )
日,甲、乙、丙、丁四地新增疑似病例数据信息如下,则一定符合该标志的是( )
甲地:总体平均数![]() ,且中位数为
,且中位数为![]() ;
;
乙地:总体平均数为![]() ,且标准差
,且标准差![]() ;
;
丙地:总体平均数![]() ,且极差
,且极差![]() ;
;
丁地:众数为![]() ,且极差
,且极差![]() .
.
A.甲地B.乙地C.丙地D.丁地
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)试探究函数![]() 在定义域内是否存在零点,若存在,请指出有几个零点;若不存在,请说明理由;
在定义域内是否存在零点,若存在,请指出有几个零点;若不存在,请说明理由;
(Ⅲ)若![]() ,且
,且![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某早餐店对一款新口味的酸奶进行了一段时间试销,定价为5元/瓶.酸奶在试销售期间足量供应,每天的销售数据按照[15,25],(25,35],(35,45],(45,55]分组,得到如下频率分布直方图,以不同销量的频率估计概率.试销结束后,这款酸奶正式上市,厂家只提供整箱批发:大箱每箱50瓶,批发成本85元;小箱每箱30瓶,批发成本65元.由于酸奶保质期短,当天未卖出的只能作废.该早餐店以试销售期间的销量作为参考,决定每天仅批发一箱(计算时每个分组取中间值作为代表,比如销量为(45,55]时看作销量为50瓶).

(1)设早餐店批发一大箱时,当天这款酸奶的利润为随机变量X,批发一小箱时,当天这款酸奶的利润为随机变量Y,求X和Y的分布列;
(2)从早餐店的收益角度和利用所学的知识作为决策依据,该早餐店应每天批发一大箱还是一小箱?(必须作出一种合理的选择)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com