
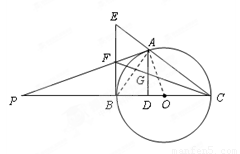
如图,点 是以线段
是以线段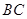 为直径的圆
为直径的圆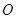 上一点,
上一点,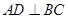 于点
于点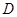 ,过点
,过点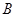 作圆
作圆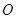 的切线,与
的切线,与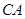 的延长线交于点
的延长线交于点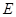 ,点
,点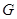 是
是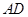 的中点,连结
的中点,连结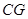 并延长与
并延长与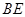 相交于点
相交于点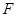 ,延长
,延长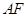 与
与 的延长线相交于点
的延长线相交于点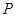 .
.

(Ⅰ)求证: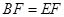 ;
;
(Ⅱ)求证: 是圆
是圆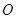 的切线.
的切线.
(Ⅰ)详见试题解析;(Ⅱ)详见试题解析.
【解析】
试题分析:(Ⅰ)由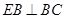 ,
,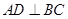 可得
可得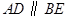 ,从而可得
,从而可得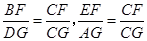
通过等量代换及题设“点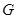 是
是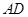 的中点”可得
的中点”可得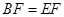 .
.
(Ⅱ)目标是要证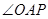 是直角,连结
是直角,连结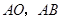 便可看出只要证得
便可看出只要证得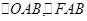 是等腰三角形即可.
是等腰三角形即可.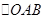 显然是等腰三角形。因为直径上的圆周角是直角,
显然是等腰三角形。因为直径上的圆周角是直角,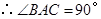 ,所以
,所以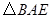 是直角三角形. 由(Ⅰ)得
是直角三角形. 由(Ⅰ)得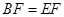 所以
所以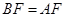 ,从而本题得证.
,从而本题得证.
试题解析:证明:(Ⅰ) 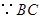 是圆
是圆 的直径,
的直径,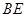 是圆
是圆 的切线,
的切线,
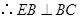 .又
.又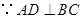 ,
,
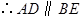 .
.
可以得知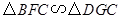 ,
, 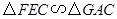 .
.
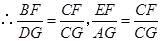 .
.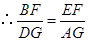 .
.
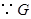 是
是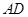 的中点,
的中点,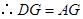 .
.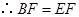 .
5分
.
5分
(Ⅱ)连结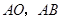 .
.
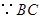 是圆
是圆 的直径,
的直径,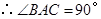 .
.
在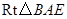 中,由(Ⅰ)得知
中,由(Ⅰ)得知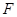 是斜边
是斜边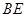 的中点,
的中点,
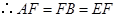 .
.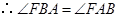 .
.
又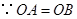 ,
,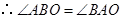 .
.
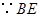 是圆
是圆 的切线,
的切线,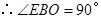
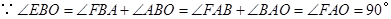 ,
,
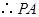 是圆
是圆 的切线. 10分
的切线. 10分
考点:1、相似三角形;2、圆的性质;3、等量代换;4、直角三角形斜边上的中线;5、几何证明


科目:高中数学 来源: 题型:
 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.| AF |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,成都市准备在南湖的一侧修建一条直路EF,另一侧修建一条观光大道,大道的前一部分为曲线段FBC,该曲线段是函数y=Asin(ωx+
如图,成都市准备在南湖的一侧修建一条直路EF,另一侧修建一条观光大道,大道的前一部分为曲线段FBC,该曲线段是函数y=Asin(ωx+| 2π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
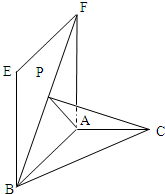 (2008•湖北模拟)如图,直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=2
(2008•湖北模拟)如图,直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=2| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年潍坊市六模) (12分) 如图,直三棱柱![]() 中,底面是以∠ABC为直角的等腰直角三角形,
中,底面是以∠ABC为直角的等腰直角三角形,
AC=2a,![]() =3a,D为
=3a,D为![]() 的中点,E为
的中点,E为![]() 的中点.
的中点.
(1)求直线BE与![]() 所成的角;
所成的角;
(2)在线段![]() 上是否存在点F,使CF⊥平面
上是否存在点F,使CF⊥平面![]() ,若存在,求出
,若存在,求出![]() ;若不存在,说明理由.
;若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
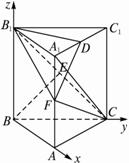
(1)求直线BE与A1C所成的角的余弦值.
(2)在线段AA1上是否存在点F,使CF⊥平面B1DF?若存在,求出|AF|;若不存在,请说明?理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com