【题目】已知函数f（x）=2sinx（sinx+cosx）.
（1）求函数的最大值；
（2）求该函数在区间[
]上的单调递增区间.
【答案】（1）
；（2）[
，
].
【解析】
（1）利用二倍角的正弦、余弦公式以及辅助角公式，将函数f（x）化为
sin（2x
）+1的形式，利用三角函数的性质即可求解.
（2）利用正弦函数的单调增区间[2kπ
，2kπ
]，k∈Z，整体代入即可求解.
（1）由题意，
f（x）=2sinx（sinx+cosx）=2sin2x+2sinxcosx
=1﹣cos2x+sin2x
=sin2x﹣cos2x+1
sin（2x）+1.
∴函数f（x）的最大值为
1.
（2）由题意，正弦函数的单调递增区间为[2kπ，2kπ]，k∈Z.
则有2kπ
2x
2kπ，k∈Z.
化简，得kπ
x
kπ
，k∈Z.
根据题意，x
，
∴该函数在区间[
]上的单调递增区间为[
，
].
科目：高中数学 来源： 题型：
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程，下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是（ ）
A. 消耗1升汽油，乙车最多可行驶5千米
B. 以相同速度行驶相同路程，三辆车中，甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时，消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下，在该市用丙车比用乙车更省油
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列有关命题的说法正确的有（ ）
（1）若p∧q为假命题，则p、q均为假命题；
（2）“x＝1”是“x2﹣3x+2＝0”的充分不必要条件；
（3）若“p∨q”为假命题，则“￢p∧￢q”为真命题．
（4）命题“若x2﹣3x+2＝0，则x＝1”的逆否命题为：“若x≠1，则x2﹣3x+2≠0”
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一般地，对于直线
及直线
外一点
，我们有点到直线
的距离公式为：
”
（1）证明上述点到直线的距离公式
（2）设直线
，试用上述公式求坐标原点
到直线距离的最大值及取最大值时
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为比较甲乙两地某月12时的气温状况，选取该月5天中12时的气温数据（单位:
）制成如图所示的茎叶图，考虑以下结论:
①甲地该月12时的平均气温低于乙地该月12时的平均气温；
②甲地该月12时的平均气温高于乙地该月12时的平均气温；
③甲地该月12时的气温的标准差小于乙地该月12时的气温的标准差；
④甲地该月12时的气温的标准差大于乙地该月12时的气温的标准差.
其中根据茎叶图能得到的统计结论的编号为（ ）
A.①③B.②③C.①④D.②④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列说法中正确的是（ ）
A. “
”是“
”成立的充分不必要条件
B. 命题
，则
C. 为了了解800名学生对学校某项教改试验的意见，用系统抽样的方法从中抽取一个容量为40的样本，则分组的组距为40
D. 已知回归直线的斜率的估计值为1.23，样本点的中心为
，则回归直线方程为
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为降低汽车尾气的排放量，某厂生产甲乙两种不同型号的节排器，分别从甲乙两种节排器中各自抽取100件进行性能质量评估检测，综合得分情况的频率分布直方图如图所示.
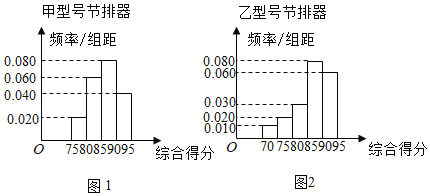
节排器等级及利润如表格表示，其中
综合得分 | 节排器等级 | 节排器利润率 |
| 一级品 |
|
| 二级品 |
|
| 三级品 |
|
（1）若从这100件甲型号节排器按节排器等级分层抽样的方法抽取10件，再从这10件节排器中随机抽取3件，求至少有2件一级品的概率；
（2）视频率分布直方图中的频率为概率，用样本估计总体，则
①若从乙型号节排器中随机抽取3件，求二级品数
的分布列及数学期望
；
②从长期来看，骰子哪种型号的节排器平均利润较大？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，椭圆
： 
的离心率为
，焦距为
.
（Ⅰ）求椭圆
的方程；
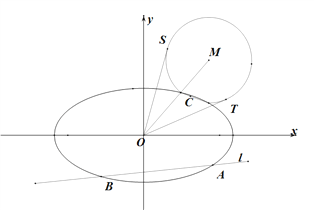
（Ⅱ）如图，动直线
： 
交椭圆
于
两点， 
是椭圆
上一点，直线
的斜率为
，且
， 
是线段
延长线上一点，且
， 
的半径为
， 
是
的两条切线，切点分别为
.求
的最大值，并求取得最大值时直线
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
