
(1)求侧棱与底面所成的角(结果用反三角表示);?
(2)求四棱锥A—BCEF的体积.
解析:(1)取AD、BC、AC中点M、N、O,连结PN、GN、PO.
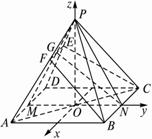
以O为坐标原点,直线ON、OP分别为y轴、z轴建立空间坐标系O—xyz.设P(0,0,t)(t>0),则A(3,-3,0),D(-3,-3,0),B(3,3,0),C(-3,3,0),F(1,-1,![]() t),
t),
∴![]() =(3,-3,-t),
=(3,-3,-t),![]() =(-6,0,0),FB=(2,4,-
=(-6,0,0),FB=(2,4,-![]() t),
t),![]() =(-6,0,0).
=(-6,0,0).
设平面P![]() 的法向量m=(a,b,1),平面
的法向量m=(a,b,1),平面![]()
![]() 的法向量n=(c,d,1),?
的法向量n=(c,d,1),?
由m·![]() =0,m·
=0,m·![]() =0,得a=0,b=-
=0,得a=0,b=-![]() .?
.?
∴m=(0,- ![]() ,1).?
,1).?
由n·FB=0,n·![]() =0,得c=0,d=
=0,得c=0,d=![]() .?
.?
∴n=(0, ![]() ,1).?
,1).?
又平面PAD⊥平面BCEF,?
∴m·n=0,则t=3![]() .
.
∴P(0,0,3![]() ).?
).?
∴![]() =(0,0,3
=(0,0,3![]() ),
),![]() =(3,-3,-3
=(3,-3,-3![]() ).
).
∴cos〈![]() ,
,![]() 〉=
〉=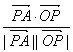 =
=![]() .
.
∴侧棱PA与底面ABCD成45°角.
(2)n=(0, ![]() ,1),cos〈
,1),cos〈![]() ,n〉=
,n〉=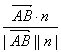 =
=![]() ,
,
∴h=|![]() |·cos〈
|·cos〈![]() ,n〉=2
,n〉=2![]() .
.
又S截面BCEF=8![]() ,?
,?
∴V A—BCEF=![]() S截面BCEF·h=16
S截面BCEF·h=16![]() .
.
温馨提示:在正棱锥中常常应用“高、侧棱、斜高、底面线段”围成的直角三角形和等腰三角形来分析线面关系.本题考查平面与平面垂直的性质定理和体积公式等.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
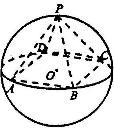 如图,正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上,点P在球面上,如果VP-ABCD=
如图,正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上,点P在球面上,如果VP-ABCD=| 16 |
| 3 |
| A、4π | B、8π |
| C、12π | D、16π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com