Question

【题目】某种植园在芒果临近成熟时，随机从一些芒果树上摘下100个芒果，其质量分别在，，，，，（单位：克）中，经统计得频率分布直方图如图所示.

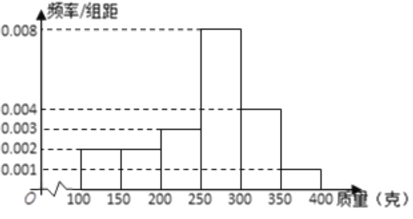
(1) 经计算估计这组数据的中位数；

(2)现按分层抽样从质量为，的芒果中随机抽取个，再从这个中随机抽取个，求这个芒果中恰有个在内的概率.

Answer 1

【答案】(1)268.75；(2).

【解析】

（1）根据频率分布直方图，找到频率总和为时对应的质量，这个质量大小就是中位数；（2）先用分层抽样计算出和中的芒果数；然后对每个芒果进行标记，采用枚举法列出所有情况，最后用古典概率模型计算目标事件概率.

（1）由频率分布直方图可知，前三组频率之和为：，第四组频率为：； 所以中位数为：；

（2）抽取的6个芒果中，质量在和内的分别有4个和2个.

设质量在内的4个芒果分别为，质量在内的2个芒果分别为. 从这6个芒果中选出3个的情况共有，，，，，，，，，，，，，，，，，，

，共计20种，其中恰有一个在内的情况有，，，，，，，，，，，共计12种，因此概率.