
【题目】如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB= ![]() PD.
PD.
(Ⅰ)证明:平面PQC⊥平面DCQ
(Ⅱ)求二面角Q﹣BP﹣C的余弦值.
【答案】解:如图,以D为坐标原点,线段DA的长为单位长,射线DA为x轴的正半轴建立空间直角坐标系D﹣xyz;
(Ⅰ)依题意有Q(1,1,0),C(0,0,1),P(0,2,0);
则 ![]() =(1,1,0),
=(1,1,0), ![]() =(0,0,1),
=(0,0,1), ![]() =(1,﹣1,0),
=(1,﹣1,0),
所以 ![]()
![]() =0,
=0, ![]()
![]() =0;
=0;
即PQ⊥DQ,PQ⊥DC,
故PQ⊥平面DCQ,
又PQ平面PQC,所以平面PQC⊥平面DCQ;
(Ⅱ)依题意,有B(1,0,1),![]() =(1,0,0),
=(1,0,0), ![]() =(﹣1,2,﹣1);
=(﹣1,2,﹣1);
设 ![]() =(x,y,z)是平面的PBC法向量,
=(x,y,z)是平面的PBC法向量,
则  即
即 ![]() ,
,
因此可取 ![]() =(0,﹣1,﹣2);
=(0,﹣1,﹣2);
设 ![]() 是平面PBQ的法向量,则
是平面PBQ的法向量,则 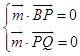 ,
,
可取 ![]() =(1,1,1),
=(1,1,1),
所以cos< ![]() ,
, ![]() >=﹣
>=﹣ ![]() ,
,
故二面角角Q﹣BP﹣C的余弦值为﹣ ![]() .
.
【解析】首先根据题意以D为坐标原点,线段DA的长为单位长,射线DA为x轴的正半轴建立空间直角坐标系D﹣xyz;
(Ⅰ)根据坐标系,求出 ![]() 、
、 ![]() 、
、 ![]() 的坐标,由向量积的运算易得
的坐标,由向量积的运算易得 ![]()
![]() =0,
=0, ![]()
![]() =0;进而可得PQ⊥DQ,PQ⊥DC,由面面垂直的判定方法,可得证明;(Ⅱ)依题意结合坐标系,可得B、
=0;进而可得PQ⊥DQ,PQ⊥DC,由面面垂直的判定方法,可得证明;(Ⅱ)依题意结合坐标系,可得B、 ![]() 、
、 ![]() 的坐标,进而求出平面的PBC的法向量
的坐标,进而求出平面的PBC的法向量 ![]() 与平面PBQ法向量
与平面PBQ法向量 ![]() ,进而求出cos<
,进而求出cos< ![]() ,
, ![]() >,根据二面角与其法向量夹角的关系,可得答案.
>,根据二面角与其法向量夹角的关系,可得答案.


科目:高中数学 来源: 题型:
【题目】设数列{an}的首项a1为常数,且an+1=3n﹣2an , (n∈N*)
(1)证明:{an﹣ ![]() }是等比数列;
}是等比数列;
(2)若a1= ![]() ,{an}中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由.
,{an}中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由.
(3)若{an}是递增数列,求a1的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=﹣ ![]() sinx
sinx ![]() cosx+1 (Ⅰ)求函数f(x)的最小正周期和单调递增区间;
cosx+1 (Ⅰ)求函数f(x)的最小正周期和单调递增区间;
(Ⅱ)若x∈[0, ![]() ],且f(x)=
],且f(x)= ![]() ,求cosx的值.
,求cosx的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂每日生产一种大型产品1件,每件产品的投入成本为2000元.产品质量为一等品的概率为![]() ,二等品的概率为
,二等品的概率为![]() ,每件一等品的出厂价为10000元,每件二等品的出厂价为8000元.若产品质量不能达到一等品或二等品,除成本不能收回外,没生产一件产品还会带来1000元的损失.
,每件一等品的出厂价为10000元,每件二等品的出厂价为8000元.若产品质量不能达到一等品或二等品,除成本不能收回外,没生产一件产品还会带来1000元的损失.
(1)求在连续生产3天中,恰有一天生产的两件产品都为一等品的的概率;
(2)已知该厂某日生产的2件产品中有一件为一等品,求另一件也为一等品的概率;
(3)求该厂每日生产该种产品所获得的利润![]() (元)的分布列及数学期望.
(元)的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() 为自然对数的底数),
为自然对数的底数),![]() ,
, ![]() .
.
(1)若![]() 是
是![]() 的极值点,且直线
的极值点,且直线![]() 分别与函数
分别与函数![]() 和
和![]() 的图象交于
的图象交于![]() ,求
,求![]() 两点间的最短距离;
两点间的最短距离;
(2)若![]() 时,函数
时,函数![]() 的图象恒在
的图象恒在![]() 的图象上方,求实数
的图象上方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:方程x2+y2﹣ax+y+1=0表示圆;命题q:方程2ax+(1﹣a)y+1=0表示斜率大于1的直线,若p∨q为真命题,p∧q为假命题,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,F1 , F2是双曲线C: ![]() (a>0,b>0)的左、右焦点,过F1的直线l与C的左、右两支分别交于A,B两点.若△ABF2为等边三角形,则双曲线的离心率为( )
(a>0,b>0)的左、右焦点,过F1的直线l与C的左、右两支分别交于A,B两点.若△ABF2为等边三角形,则双曲线的离心率为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB= ![]() ,BC=1,P为△ABC内一点,∠BPC=90°.
,BC=1,P为△ABC内一点,∠BPC=90°. 
(1)若PB= ![]() ,求PA;
,求PA;
(2)若∠APB=150°,求tan∠PBA.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com