
已知函数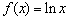 ,
,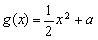 (
(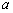 为常数),直线
为常数),直线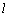 与函数
与函数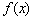 、
、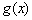 的图象都相切,且
的图象都相切,且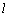 与函数
与函数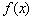 图象的切点的横坐标为
图象的切点的横坐标为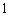 .
.
(1)求直线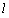 的方程及
的方程及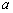 的值;
的值;
(2)若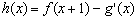 [注:
[注: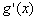 是
是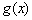 的导函数],求函数
的导函数],求函数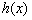 的单调递增区间;
的单调递增区间;
(3)当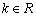 时,试讨论方程
时,试讨论方程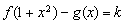 的解的个数.
的解的个数.
(1) 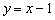 ;
; 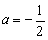 ;(2)
;(2)  ,
,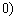 ;(3)详见解析.
;(3)详见解析.
【解析】
试题分析:(1)利用函数在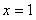 处的导数,等于在
处的导数,等于在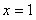 处切线的斜率,所以先求
处切线的斜率,所以先求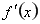 ,再求
,再求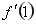 ,直线
,直线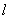 的斜率就是
的斜率就是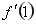 ,直线
,直线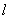 过点
过点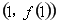 ,代入得到直线
,代入得到直线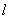 的方程,直线
的方程,直线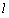 与
与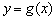 的图象相切,所以代入联立
的图象相切,所以代入联立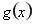 ,
, 得到
得到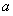 值;(2)先求
值;(2)先求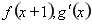 , 得到
, 得到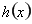 ,再求
,再求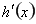 ,令
,令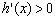 ,得到
,得到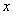 的取值范围,即求得函数
的取值范围,即求得函数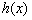 的单调递增区间;(3)令
的单调递增区间;(3)令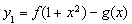
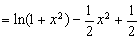 ,
,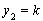 ,再求
,再求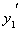 ,得到极值点,然后列表分析当
,得到极值点,然后列表分析当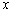 变化时,
变化时,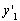 ,
,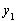 的变化情况,结合
的变化情况,结合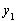 为偶函数,画出
为偶函数,画出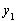 的函数图形,再画
的函数图形,再画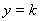 ,当直线
,当直线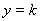 上下变化时,可以看出交点的变化,根据交点的不同,从而确定,再不同
上下变化时,可以看出交点的变化,根据交点的不同,从而确定,再不同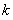 的范围下得到不同的交点个数.此问注意分类讨论思想的使用,不要遗漏情况.属于较难习题.
的范围下得到不同的交点个数.此问注意分类讨论思想的使用,不要遗漏情况.属于较难习题.
试题解析:(1)解:由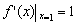 ,
,
故直线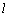 的斜率为
的斜率为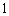 ,切点为
,切点为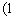 ,
,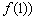 ,即
,即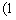 ,
,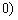 ,
,
所以直线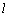 的方程为
的方程为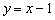 . 3分
. 3分
直线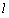 与
与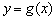 的图象相切,等价于方程组
的图象相切,等价于方程组 只有一解,
只有一解,
即方程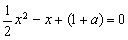 有两个相等实根,
有两个相等实根,
所以令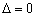 ,解得
,解得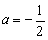 . 5分
. 5分
(2)因为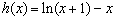
 ,
,
由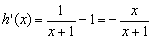 ,
,
令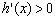 ,所以
,所以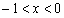 ,
,
所以函数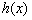 的单调递增区间是
的单调递增区间是 ,
,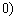 . 8分
. 8分
(3)令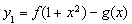
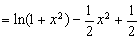 ,
,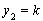 ,
,
由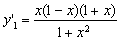 ,令
,令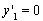 ,得
,得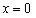 ,
,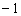 ,
,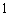 , 10分
, 10分
当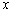 变化时,
变化时,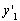 ,
,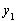 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
| + |
| - |
| + |
| - |
|
| 极大值 |
| 极小值 |
| 极大值 |
|
又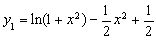 为偶函数, 所以函数
为偶函数, 所以函数 的图象如图:
的图象如图:
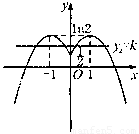
当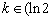 ,
, 时,方程无解;
时,方程无解;
当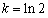 或
或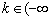 ,
,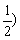 时,方程有两解;
时,方程有两解;
当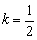 时,方程有三解;
时,方程有三解;
当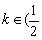 ,
,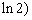 时,方程有四解. 14分
时,方程有四解. 14分
考点:1.导数的几何意义;2.利用函数的导数求函数的单调区间;3.利用导数求方程根的个数;4.数形结合.


科目:高中数学 来源: 题型:
(09年江宁中学三月)(16分)已知函数![]() ,
,![]() (
(![]() 为常数).函数
为常数).函数![]() 定义为:对每个给定的实数
定义为:对每个给定的实数![]() ,
,![]()
(1)求![]() 对所有实数
对所有实数![]() 成立的充分必要条件(用
成立的充分必要条件(用![]() 表示);
表示);
(2)设![]() 是两个实数,满足
是两个实数,满足![]() ,且
,且![]() .若
.若![]() ,求证:函数
,求证:函数![]() 在区间
在区间![]() 上的单调增区间的长度之和为
上的单调增区间的长度之和为![]() (闭区间
(闭区间![]() 的长度定义为
的长度定义为![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题12分)已知函数![]() (m为常数,m>0)有极大值9.
(m为常数,m>0)有极大值9.
(1)求m的k*s#5^u值;
(2)若斜率为-5的k*s#5^u直线是曲线![]() 的k*s#5^u切线,求此直线方程.
的k*s#5^u切线,求此直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com