
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬AC=BC=a����P�ڱ�AB�ϣ��� ![]() =��
=�� ![]() ���ˣ�0��������P��PE��BC��AC��E����PF��AC��BC��F����PE����APE���۳ɡ�A��PE��ʹƽ��A��PE��ƽ��ABC����PF����BPF���۳ɡ�B��PF��ʹƽ��B��PF��ƽ��ABC��
���ˣ�0��������P��PE��BC��AC��E����PF��AC��BC��F����PE����APE���۳ɡ�A��PE��ʹƽ��A��PE��ƽ��ABC����PF����BPF���۳ɡ�B��PF��ʹƽ��B��PF��ƽ��ABC�� 
��1����֤��B��C��ƽ��A��PE��
��2���Ƿ������ʵ���ˣ�ʹ�ö����C��A��B�䩁P�Ĵ�СΪ60�㣿�����ڣ�����˵�ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1��֤������FC��PE��FCƽ��A'PE����FC��ƽ��A'PE��
��ƽ��A'PE��ƽ��ABC����A'E��PE����A'E��ƽ��ABC��
ͬ����B'F��ƽ��ABC����B'F��A'E���Ӷ�B'F��ƽ��A'PE��
��ƽ��B'CF��ƽ��A'PE���Ӷ�B'C��ƽ��A'PE��
��2���⣺������ʵ����= ![]() ��ʹ�ö����C��A��B�䩁P�Ĵ�СΪ60�㣮
��ʹ�ö����C��A��B�䩁P�Ĵ�СΪ60�㣮
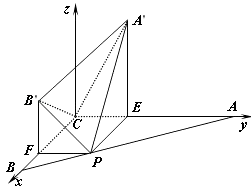
��ʵ�ϣ���CΪԭ�㣬CB����ֱ��Ϊx�ᣬCA����ֱ��Ϊy�ᣬ��C�Ҵ�ֱ��ƽ��ABC��ֱ��Ϊz�ᣬ�����ռ�ֱ������ϵ����ͼ��
��AC=BC=a���� ![]() =��
=�� ![]() ���ˣ�0����
���ˣ�0����
��C��0��0��0����A�䣨0�� ![]() ��
�� ![]() ����B�䣨
����B�䣨 ![]() ��0��
��0�� ![]() ����P��
����P�� ![]() ��
�� ![]() ��0����
��0����
�� ![]() =��0��
=��0�� ![]() ��
�� ![]() ����
���� ![]() =��
=�� ![]() ����
���� ![]() ��
�� ![]() ����
���� ![]() =��0��
=��0�� ![]() ����
���� ![]() ����
����
ƽ��CA'B'��һ�������� ![]() =��
=�� ![]() ���ˣ���1����ƽ��PA'B'��һ��������
���ˣ���1����ƽ��PA'B'��һ�������� ![]() =��1��1��1����
=��1��1��1����
�� ![]() =
=  =cos60��=
=cos60��= ![]() ��
��
����� ![]() ��8��+9=0����æ�=
��8��+9=0����æ�= ![]() ��
��
�������ʵ����= ![]() ��ʹ�ö����C��A��B�䩁P�Ĵ�СΪ60�㣮
��ʹ�ö����C��A��B�䩁P�Ĵ�СΪ60�㣮
����������1����������ƽ�е��ж���������֤��FC��ƽ��A'PE�����������洹ֱ�����ʶ�������֤��B��F��A��E�������õ�B'F��ƽ��A'PE����������ƽ�е��ж��������ɵõ� ƽ��B'CF��ƽ��A'PE���Ӷ��õ�����ƽ�У���2��ͨ�������ռ�ֱ������ϵ������֪��� ![]() =��
=�� ![]() ���ˣ�0��������õ�����꣬�Ѷ����C��A��B�䩁P�Ĵ�СΪ60��ת��Ϊ����ƽ��ķ������ļн���ʽ��æ˵�ֵ��
���ˣ�0��������õ�����꣬�Ѷ����C��A��B�䩁P�Ĵ�СΪ60��ת��Ϊ����ƽ��ķ������ļн���ʽ��æ˵�ֵ��
�����㾫��������ֱ����ƽ��ƽ�е��ж�����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪ƽ����һ��ֱ�����ƽ���ڵ�һ��ֱ��ƽ�У����ֱ�����ƽ��ƽ�У����Ϊ������ƽ�У�������ƽ�У�


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ��ԭ��OΪ���㣬x���������Ϊ���ᣬ����������ϵȡ��ȵij��ȵ�λ����ֱ֪��l�IJ�������Ϊ ![]() ��tΪ������0�������У�������C�ļ����귽��Ϊ��sin2��=4cos�ȣ� ����������C��ֱ�����귽�̣�
��tΪ������0�������У�������C�ļ����귽��Ϊ��sin2��=4cos�ȣ� ����������C��ֱ�����귽�̣�
������ֱ��l������C�ཻ��A��B���㣬�����仯ʱ����|AB|����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У��ڽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c����2asinB= ![]() b��
b��
��1�����A�Ĵ�С��
��2����0��A�� ![]() ��a=6���ҡ�ABC�����S=
��a=6���ҡ�ABC�����S= ![]() �����ABC���ܳ���
�����ABC���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() x3��
x3�� ![]() x2+logax����a��0��a��1��Ϊ�������ϵ���������f'��x���Ǻ���f��x���ĵ�������f'��x������СֵС�ڵ���0�� ������a��ֵ��
x2+logax����a��0��a��1��Ϊ�������ϵ���������f'��x���Ǻ���f��x���ĵ�������f'��x������СֵС�ڵ���0�� ������a��ֵ��
�����躯�� ![]() ����g��x1��+g��x2��=0����֤��
����g��x1��+g��x2��=0����֤�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��PΪ����f��x��=lnx��ͼ��������һ�㣬��QΪԲ ![]() ������һ�㣬���߶�PQ���ȵ���СֵΪ�� ��
������һ�㣬���߶�PQ���ȵ���СֵΪ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ�ϳƺ���y=kx+b��k��b��R��k��0��Ϊ���Ժ��������ڷ����Կɵ�����f��x�����ڵ�x0����һ��x�ĺ���ֵf��x�������������·���������ƴ���ֵ��f��x����f��x0��+f'��x0����x��x0����������һ������ ![]() �Ľ��ƴ���ֵ�� ��
�Ľ��ƴ���ֵ�� ��
A.����m
B.��m
C.����m
D.��m�Ĵ�С��ϵ��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|2x��1|+|ax��5|��0��a��5����
��1����a=1ʱ����ʽf��x����9�Ľ⼯��
��2���������y=f��x������СֵΪ4����ʵ��a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ⳤΪ1��������ABCD��A1B1C1D1�У�AC��BD=O��E���߶�B1C�����˵㣩�ϵ�һ���㣬�� ��OE��BD1��
��OE����A1C1D��
������A1��BDE�����Ϊ��ֵ��
��OE��A1C1���ɵ�����Ϊ90�㣮
������������ȷ�ĸ����ǣ� ��
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������{an}��ǰn���Sn=3n2+2n+1��
��1����{an}��ͨ�ʽ��
��2����bn=an2n �� ��{bn}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com