
【题目】【2017江西师范大学附属中学三模】已知函数![]() 是自然对数的底数).
是自然对数的底数).
(1)求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,当
,当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(3)若![]() 且
且![]() ,求证:
,求证: ![]() .
.
【答案】(1)![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)![]() (3)见解析
(3)见解析
【解析】试题分析:(1) 求出![]() ,
, ![]() 得增区间,
得增区间, ![]() 得减区间;(2)利用导数研究函数
得减区间;(2)利用导数研究函数![]() 的单调性即可求函数
的单调性即可求函数![]() 的最大值;(3)化简已知得
的最大值;(3)化简已知得![]() ,
, ![]()
![]() 即
即![]() ,然后利用分析法证明原不等式.
,然后利用分析法证明原不等式.
试题解析: (1) ![]() 的定义域为
的定义域为![]() ,且
,且![]() ,
,
令![]() ,
, ![]()
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2) ![]() ,
,
![]() ,
,
当![]() 时,
时, ![]() ,
,![]() ,
,![]()
当![]() 时,
时, ![]() ,
,![]()
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
![]() .
.
(3) ![]() ,
, ![]()
![]() 即
即![]() .
.
由(1)知 ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,且
上单调递减,且![]() ,
,
则![]()
要证![]() ,即证
,即证![]() ,即证
,即证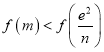 ,即证
,即证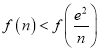 ,
,
即证![]() ,由于
,由于![]() ,即证
,即证![]() .
.
令![]()
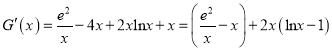
![]()
![]()
![]() 恒成立
恒成立
![]() 在
在![]() 递增,
递增, ![]() 在
在![]() 恒成立,
恒成立,
![]() 原不等式成立.
原不等式成立.
【方法点晴】本题主要考查的是利用导数研究函数的单调性、利用导数研究函数的最值、不等式的恒成立,属于难题.利用导数研究函数![]() 的单调性进一步求函数最值的步骤:①确定函数
的单调性进一步求函数最值的步骤:①确定函数![]() 的定义域;②对
的定义域;②对![]() 求导;③令
求导;③令![]() ,解不等式得
,解不等式得![]() 的范围就是递增区间;令
的范围就是递增区间;令![]() ,解不等式得
,解不等式得![]() 的范围就是递减区间;④根据单调性求函数
的范围就是递减区间;④根据单调性求函数![]() 的极值及最值(闭区间上还要注意比较端点处函数值的大小).
的极值及最值(闭区间上还要注意比较端点处函数值的大小).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知△ABC的三边长为a,b,c,则下列命题中真命题是( )
A.“a2+b2>c2”是“△ABC为锐角三角形”的充要条件
B.“a2+b2<c2”是“△ABC为钝角三角形”的必要不充分条件
C.“a3+b3=c3”是“△ABC为锐角三角形”的既不充分也不必要条件
D.“ ![]() +
+ ![]() =
= ![]() ”是“△ABC为钝角三角形”的充分不必要条件
”是“△ABC为钝角三角形”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中装有各色球12只,其中5个红球,4个黑球,2个白球,1个绿球;从中随机取出1球.求:
(1)取出的1球是红球或黑球的概率;
(2)取出的1球是红球或黑球或白球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设偶函数f(x)的定义域为[﹣4,0)∪(0,4],若当x∈(0,4]时,f(x)=log2x,
(1)求出函数在定义域[﹣4,0)∪(0,4]的解析式;
(2)求不等式xf(x)<0得解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017衡阳第二次联考】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)如果对于任意的![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,
, ![]() ,过点
,过点![]() 作函数
作函数![]() 的图象的所有切线,令各切点的横坐标按从小到大构成数列
的图象的所有切线,令各切点的横坐标按从小到大构成数列![]() ,求数列
,求数列![]() 的所有项之和的值.
的所有项之和的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.某厂一批产品的次品率为![]() , 则任意抽取其中10件产品一定会发现一件次品
, 则任意抽取其中10件产品一定会发现一件次品
B.气象部门预报明天下雨的概率是90%,说明明天该地区90%的地方要下雨,其余10%的地方不会下雨
C.某医院治疗一种疾病的治愈率为10%,那么前9个病人都没有治愈,第10个人就一定能治愈
D.掷一枚硬币,连续出现5次正面向上,第六次出现反面向上的概率与正面向上的概率仍然都为0.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某试验田分别种植了甲乙两种水稻,为了研究这两种水稻的产量,抽检了甲、乙两种水稻的谷穗各1000株.经统计,得到每株谷穗的粒数的频率分布直方图如图: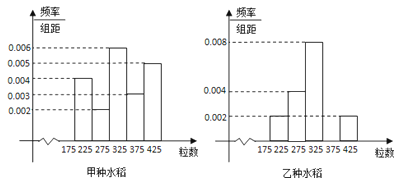
(Ⅰ)求乙种水稻谷穗的粒数落在[325,375)之间的频率,并将频率分布直方图补齐;
(Ⅱ)试根据频率分布直方图估计甲种水稻谷穗粒数的中位数与平均数(精确到0.1);
(Ⅲ)根据频率分布直方图,请至少从两方面对甲乙两种水稻谷穗的粒数作出评价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com