
【题目】【2017广东佛山二模】设函数![]() ,其中
,其中![]() ,
,![]() 是自然对数的底数.
是自然对数的底数.
(Ⅰ)若![]() 是
是![]() 上的增函数,求
上的增函数,求![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() ,证明:
,证明:![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】试题分析:(I)由于函数单调递增,故导函数恒为非负数,分离常数后利用导数求得![]() 的最小值,由此得到
的最小值,由此得到![]() 的取值范围;(II)将原不等式
的取值范围;(II)将原不等式![]() ,转化为
,转化为![]() ,令
,令![]() ,求出
,求出![]() 的导数,对
的导数,对![]() 分成
分成![]() 两类,讨论函数的最小值,由此证得
两类,讨论函数的最小值,由此证得![]() ,由此证得
,由此证得![]() .
.
试题解析:
(Ⅰ)![]() ,
,![]() 是
是![]() 上的增函数等价于
上的增函数等价于![]() 恒成立.
恒成立.
令![]() ,得
,得![]() ,令
,令![]() (
(![]() ).以下只需求
).以下只需求![]() 的最大值.
的最大值.
求导得![]() ,
,
令![]() ,
,![]() ,
,![]() 是
是![]() 上的减函数,
上的减函数,
又![]() ,故1是
,故1是![]() 的唯一零点,
的唯一零点,
当![]() ,
,![]() ,
,![]() ,
,![]() 递增;当
递增;当![]() ,
,![]() ,
,![]() ,
,![]() 递减;
递减;
故当![]() 时,
时,![]() 取得极大值且为最大值
取得极大值且为最大值![]() ,
,
所以![]() ,即
,即![]() 的取值范围是
的取值范围是![]() .
.
(Ⅱ)![]()
![]() .
.
令![]() (
(![]() ),以下证明当
),以下证明当![]() 时,
时,![]() 的最小值大于0.
的最小值大于0.
求导得![]()
![]() .
.
①当![]() 时,
时,![]() ,
,![]()
![]() ;
;
②当![]() 时,
时,![]()
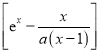 ,令
,令![]() ,
,
则![]()
![]() ,又
,又![]()
![]() ,
,
取![]() 且使
且使![]() ,即
,即![]() ,则
,则![]()
![]() ,
,
因为![]() ,故
,故![]() 存在唯一零点
存在唯一零点![]() ,
,
即![]() 有唯一的极值点且为极小值点
有唯一的极值点且为极小值点![]() ,又
,又![]() ,
,
且![]() ,即
,即![]() ,故
,故![]() ,
,
因为![]() ,故
,故![]() 是
是![]() 上的减函数.
上的减函数.
所以![]()
![]() ,所以
,所以![]() .
.
综上,当![]() 时,总有
时,总有![]() .
.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】为迎接“双十一”活动,某网店需要根据实际情况确定经营策略.
(1)采购员计划分两次购买一种原料,第一次购买时价格为a元/个,第二次购买时价格为b元/个(其中a≠b).该采购员有两种方案:方案甲:每次购买m个;方案乙:每次购买n元.请确定按照哪种方案购买原料平均价格较小.
(2)“双十一”活动后,网店计划对原价为100元的商品两次提价,现有两种方案:方案丙:第一次提价p,第二次提价q;方案丁:第一次提价 ![]() ,第二次提价
,第二次提价 ![]() ,(其中p≠q)请确定哪种方案提价后价格较高.
,(其中p≠q)请确定哪种方案提价后价格较高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( ) 
A.588
B.480
C.450
D.120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆N经过点A(3,1),B(﹣1,3),且它的圆心在直线3x﹣y﹣2=0上.
(Ⅰ)求圆N的方程;
(Ⅱ)求圆N关于直线x﹣y+3=0对称的圆的方程.
(Ⅲ)若点D为圆N上任意一点,且点C(3,0),求线段CD的中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正项数列{an}的前n项和Sn满足:Sn2﹣(n2+n﹣1)Sn﹣(n2+n)=0
(1)求数列{an}的通项公式an;
(2)令bn= ![]() ,求数列{bn}的前n项和Tn , 证明:对于任意的n∈N* , 都有Tn
,求数列{bn}的前n项和Tn , 证明:对于任意的n∈N* , 都有Tn ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx﹣x2 , a∈R,
(1)求函数f(x)的单调区间;
(2)若x≥1时,f(x)≤0恒成立,求实数a的取值范围;
(3)设a>0,若A(x1 , y1),B(x2 , y2)为曲线y=f(x)上的两个不同点,满足0<x1<x2 , 且x3∈
(x1 , x2),使得曲线y=f(x)在x=x3处的切线与直线AB平行,求证:x3< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= ![]() ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点. 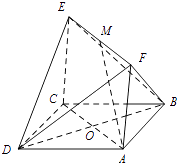
(1)求证:AM∥平面BDE;
(2)求证:AM⊥平面BDF;
(3)求A点到面BDF的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】100辆汽车通过某一段公路时,时速的频率分布直方图如图所示,则时速在[50,70)的汽车大约有( )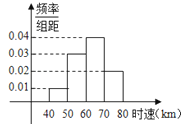
A.60辆
B.80辆
C.70辆
D.140辆
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com