
【题目】一艘船在航行过程中发现前方的河道上有一座圆拱桥.在正常水位时,拱桥最高点距水面8m,拱桥内水面宽32m,船只在水面以上部分高6.5m,船顶部宽8m,故通行无阻,如图所示. 
(1)建立适当的平面直角坐标系,求正常水位时圆弧所在的圆的方程;
(2)近日水位暴涨了2m,船已经不能通过桥洞了.船员必须加重船载,降低船身在水面以上的高度,试问:船身至少降低多少米才能通过桥洞?(精确到0.1m, ![]() )
)
【答案】
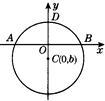
(1)解:在正常水位时,设水面与桥横截面的交线为x轴,
过拱桥最高点且与水面垂直的直线为y轴,建立平面直角坐标系,
如图所示,则A,B,D三点的坐标分别为(﹣16,0),(16,0),(0,8).
又圆心C在y轴上,故可设C(0,b).
因为|CD|=|CB|,所以 ![]() ,解得b=﹣12.
,解得b=﹣12.
所以圆拱所在圆的方程为:x2+(y+12)2=(8+12)2=202=400
(2)解:当x=4时,求得y≈7.6,即桥拱宽为8m的地方距正常水位时的水面约7.60m,距涨水后的水面约5.6m,因为船高6.5m,顶宽8m,
所以船身至少降低6.5﹣5.6=0.9(m)以上,船才能顺利通过桥洞.
【解析】(1)在正常水位时,设水面与桥横截面的交线为x轴,过拱桥最高点且与水面垂直的直线为y轴,建立平面直角坐标系建立坐标系,利用|CD|=|CB|,确定圆的方程;(2)令x=4时,求得y≈7.6,即桥拱宽为8m的地方距正常水位时的水面约7.60m,即可求得通过桥洞,船身至少应该降低多少.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ![]() . (I)当a=1时,求f(x)在x∈[1,+∞)最小值;
. (I)当a=1时,求f(x)在x∈[1,+∞)最小值;
(Ⅱ)若f(x)存在单调递减区间,求a的取值范围;
(Ⅲ)求证: ![]() (n∈N*).
(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +lnx在(1,+∞)上是增函数,且a>0.
+lnx在(1,+∞)上是增函数,且a>0.
(1)求a的取值范围;
(2)求函数g(x)=ln(1+x)﹣x在[0,+∞)上的最大值;
(3)设a>1,b>0,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知P是圆x2+y2=36的圆心,R是椭圆 ![]() 上的一动点,且满足
上的一动点,且满足 ![]() .
.
(1)求动点Q的轨迹方程
(2)若直线y=x+1与曲线Q相交于A、B两点,求弦AB的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(用空间向量坐标表示解答)已知正三棱柱ABC﹣A1B1C1的各棱长都是4,E是BC的中点,F在CC1上,且CF=1. 
(1)求证:EF⊥A1C;
(2)求二面角C﹣AF﹣E的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂生产某种产品,当年产量在150吨至250吨时,每年的生产成本y万元与年产量x吨之间的关系可可近似地表示为y= ![]() ﹣30x+4000.
﹣30x+4000.
(1)若每年的生产总成本不超过2000万元,求年产量x的取值范围;
(2)求年产量为多少吨时,每吨的平均成本最低,并求每吨的最低成本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我校为进行“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S(平方米)的矩形AMPN健身场地.如图,点M在AC上,点N在AB上,且P点在斜边BC上.已知∠ACB=60°,|AC|=30米,|AM|=x米,x∈[10,20].设矩形AMPN健身场地每平方米的造价为 ![]() 元,再把矩形AMPN以外(阴影部分)铺上草坪,每平方米的造价为
元,再把矩形AMPN以外(阴影部分)铺上草坪,每平方米的造价为 ![]() 元(k为正常数).
元(k为正常数).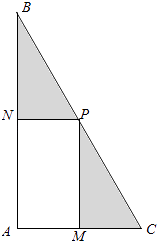
(1)试用x表示S,并求S的取值范围;
(2)求总造价T关于面积S的函数T=f(S);
(3)如何选取|AM|,使总造价T最低(不要求求出最低造价).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com