
如图,灌溉渠的横截面是等腰梯形,底宽2米,边坡的长为x米、倾角为锐角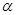 .
.
(1)当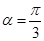 且灌溉渠的横截面面积大于8平方米时,求x的最小正整数值;
且灌溉渠的横截面面积大于8平方米时,求x的最小正整数值;
(2)当x=2时,试求灌溉渠的横截面面积的最大值.

(1)x的最小正整数值是3.
(2)灌溉渠的横截面面积的最大值是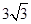 .
.
【解析】解:由已知得等腰梯形的高为xsin ,上底长为2+2xcos
,上底长为2+2xcos ,从而横截面面积S=
,从而横截面面积S=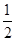 (2+2+2xcos
(2+2+2xcos )·xsin
)·xsin =x2sin
=x2sin cos
cos +2xsin
+2xsin .
.
(1)当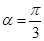 时,面积
时,面积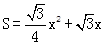 是(0,+∞)上的增函数,当x=2时,S=3
是(0,+∞)上的增函数,当x=2时,S=3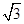 <8;当x=3时,S=
<8;当x=3时,S=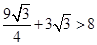 . 所以,灌溉渠的横截面面积大于8平方米时,x的最小正整数值是3.
. 所以,灌溉渠的横截面面积大于8平方米时,x的最小正整数值是3.
(2)当x=2时,S=4sin cos
cos +4sin
+4sin ,S
,S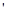 =4cos2
=4cos2 -4sin2
-4sin2 +4cos
+4cos
=4(2cos2 +cos
+cos -1)=4(2cos
-1)=4(2cos -1)·(cos
-1)·(cos +1),由S
+1),由S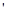 =0及
=0及 是锐角,得
是锐角,得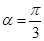 . 当0<
. 当0< <
<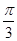 时,S
时,S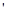 >0,S是增函数;当
>0,S是增函数;当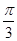 <
< <
<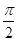 时,S
时,S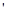 <0,S是减函数。所以,当
<0,S是减函数。所以,当 =
=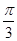 时,S有最大值
时,S有最大值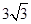 .
.
综上所述,灌溉渠的横截面面积的最大值是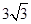 .
.


科目:高中数学 来源: 题型:
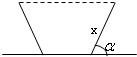 如图,灌溉渠的横截面是等腰梯形,底宽2米,边坡的长为x米、倾角为锐角α.
如图,灌溉渠的横截面是等腰梯形,底宽2米,边坡的长为x米、倾角为锐角α.| π | 3 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省连云港市灌云县陡沟中学高三(上)9月月考数学试卷(解析版) 题型:解答题
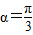 且灌溉渠的横截面面积大于8平方米时,求x的最小正整数值;
且灌溉渠的横截面面积大于8平方米时,求x的最小正整数值;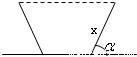
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省泰州中学高三(上)质量检测数学试卷(理科)(解析版) 题型:解答题
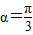 且灌溉渠的横截面面积大于8平方米时,求x的最小正整数值;
且灌溉渠的横截面面积大于8平方米时,求x的最小正整数值;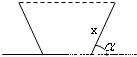
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省连云港市灌云县陡沟中学高三(上)9月月考数学试卷(解析版) 题型:解答题
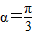 且灌溉渠的横截面面积大于8平方米时,求x的最小正整数值;
且灌溉渠的横截面面积大于8平方米时,求x的最小正整数值;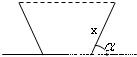
查看答案和解析>>
科目:高中数学 来源:2012年湖南省湘潭市高考数学四模试卷(理科)(解析版) 题型:解答题
 且灌溉渠的横截面面积大于8平方米时,求x的最小正整数值;
且灌溉渠的横截面面积大于8平方米时,求x的最小正整数值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com