
【题目】为了研究学生的数学核素养与抽象(能力指标![]() )、推理(能力指标
)、推理(能力指标![]() )、建模(能力指标
)、建模(能力指标![]() )的相关性,并将它们各自量化为1、2、3三个等级,再用综合指标
)的相关性,并将它们各自量化为1、2、3三个等级,再用综合指标![]() 的值评定学生的数学核心素养;若
的值评定学生的数学核心素养;若![]() ,则数学核心素养为一级;若
,则数学核心素养为一级;若![]() ,则数学核心素养为二级;若
,则数学核心素养为二级;若![]() ,则数学核心素养为三级,为了了解某校学生的数学核素养,调查人员随机访问了某校10名学生,得到如下结果:
,则数学核心素养为三级,为了了解某校学生的数学核素养,调查人员随机访问了某校10名学生,得到如下结果:
学生编号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)在这10名学生中任取两人,求这两人的建模能力指标相同的概率;
(2)从数学核心素养等级是一级的学生中任取一人,其综合指标为![]() ,从数学核心素养等级不是一级的学生中任取一人,其综合指标为
,从数学核心素养等级不是一级的学生中任取一人,其综合指标为![]() ,记随机变量
,记随机变量![]() ,求随机变量
,求随机变量![]() 的分布列及其数学期望.
的分布列及其数学期望.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:
(1)由题可知:建模能力一级的学生是![]() ;建模能力二级的学生是
;建模能力二级的学生是![]() ;建模能力三级的学生是
;建模能力三级的学生是![]() .
.
(2) 由题可知,数学核心素养一级:![]() ,数学核心素养不是一级的:
,数学核心素养不是一级的:![]() ;
;![]() 的可能取值为1,2,3,4,5. 具体如下:
的可能取值为1,2,3,4,5. 具体如下:
学生 编号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
综合 指标 | 7 | 7 | 9 | 5 | 7 | 8 | 6 | 8 | 4 | 6 |
核心素养等级 | 一级 | 一级 | 一级 | 二级 | 一级 | 一级 | 二级 | 一级 | 三级 | 二级 |
试题解析:(1)由题可知:建模能力一级的学生是![]() ;建模能力二级的学生是
;建模能力二级的学生是![]() ;建模能力三级的学生是
;建模能力三级的学生是![]() .
.
记“所取的两人的建模能力指标相同”为事件![]() ,
,
则![]()
(2)由题可知,数学核心素养一级:![]() ,数学核心素养不是一级的:
,数学核心素养不是一级的:![]() ;
;![]() 的可能取值为1,2,3,4,5.
的可能取值为1,2,3,4,5.
![]()
![]()
![]()
![]()
![]()
∴随机变量![]() 的分布列为
的分布列为
| 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
∴![]()
![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时,生产一件产品A的利润为2 100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为________________元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinxcosx+2 ![]() cos2x﹣
cos2x﹣ ![]()
(1)求函数f(x)的最小正周期和单调减区间;
(2)已知△ABC的三个内角A,B,C的对边分别为a,b,c,其中a=7,若锐角A满足f( ![]() ﹣
﹣ ![]() )=
)= ![]() ,且sinB+sinC=
,且sinB+sinC= ![]() ,求bc的值.
,求bc的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率是
的离心率是![]() ,且过点
,且过点![]() .直线
.直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)求![]() 的面积的最大值;
的面积的最大值;
(Ⅲ)设直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() .判断
.判断![]() ,
, ![]() 大小关系,并加以证明.
大小关系,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
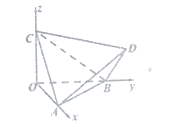
【题目】如图,正四面体![]() 的顶点
的顶点![]() 分别在两两垂直的三条射线
分别在两两垂直的三条射线![]() 上,在下列命题中,错误的是( )
上,在下列命题中,错误的是( )
A. 四面体![]() 是正三棱锥 B. 直线
是正三棱锥 B. 直线![]() 与平面
与平面![]() 相交 C. 异面直线
相交 C. 异面直线![]() 和
和![]() 所成角是
所成角是![]() D. 直线
D. 直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 定义域为
定义域为![]() ,如果存在非实数
,如果存在非实数![]() 对任意的
对任意的![]() 都有
都有![]() ,则称函数
,则称函数![]() 是“似周期函数”,非零常数
是“似周期函数”,非零常数![]() 为函数
为函数![]() 的似周期.现有下列四个关于“似周期函数”的命题:
的似周期.现有下列四个关于“似周期函数”的命题:
①如果“似周期函数”![]() 的“似周期”为
的“似周期”为![]() ,那么它是周期为
,那么它是周期为![]() 的周期函数;
的周期函数;
②函数![]() 是“似周期函数”;
是“似周期函数”;
③函数![]() 是“似周期函数”;
是“似周期函数”;
④如果函数![]() 是“似周期函数”.那么”
是“似周期函数”.那么”![]()
其中是真命题的序号是____.(请填写所有满足条件的命题序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边长分别为a,b,c,B= ![]() .
.
(1)若a=3,b= ![]() ,求c的值;
,求c的值;
(2)若f(A)=sinA( ![]() cosA﹣sinA),a=
cosA﹣sinA),a= ![]() ,求f(A)的最大值及此时△ABC的外接圆半径.
,求f(A)的最大值及此时△ABC的外接圆半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com